- 1. Պարկում կա 6 կանաչ, 14 դեղին և 4 կարմիր գնդակ։ Առանց նայելու ամենաքիչը քանի՞ գնդակ պետք է հանել, որպեսզի դրանցից գոնե մեկը լինի կանաչ։
14+4+1=19
2. Պարկում կա 5 կապույտ, 12 կանաչ և 11 դեղին գնդակ։ Առանց նայելու ամենաքիչը քանի՞ գնդակ պետք է հանել, որպեսզի դրանցից գոնե մեկը լինի կանաչ։
5+11+1=17
3. Պայուսակում կա 3 սև, 8 դեղին և 10 կարմիր մատիտ։ Առանց նայելու ամենաքիչը քանի՞ մատիտ պետք է հանել, որպեսզի դրանցից գոնե երկուսը լինի կարմիր։
3+8+2=13
4. Պայուսակում կա 7 կապույտ, 5 սպիտակ և 10 կարմիր գնդիկ։ Առանց նայելու ամենաքիչը քանի՞ գնդիկ պետք է հանել, որպեսզի դրանցից գոնե երեքը լինի կապույն։
5+10+3=18
5. Պարկում կա 7 սպիտակ, 2 դեղին և 1 սև գնդակ։ Առանց նայելու ամենաքիչը քանի՞ գնդակ պետք է հանել, որպեսզի դրանցից գոնե մեկը լինի դեղին։
7+1+1=9
Рубрика: Նախագծեր
📑Հետաքրքիր փաստեր մաթեմատիկայի մասին📑
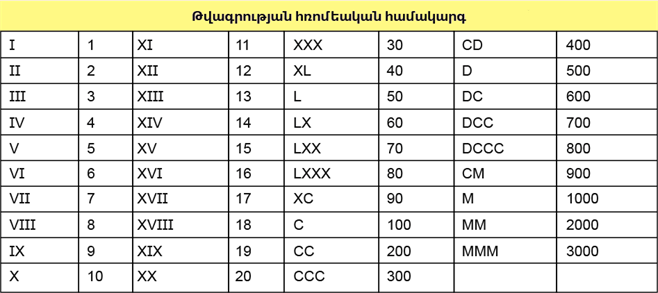
Թվերի մեծ աշխարհում․ հռոմեական թվեր
Թվերի ստեղծման պատմությունը գալիս է դեռևս անտիկ ժամանակներից։ Հաշվելու կամ հաշիվ պահելու անհրաժեշտությունն առաջացել է այն ժամանակ, երբ մարդիկ անհրաժեշտություն են ունեցել միմյանց տեղեկացնել որսի կամ գտած առարկաների քանակի մասին։ Օրինակ, երբ պետք էր որսած ձուկը փոխանակել դանակի հետ, պարզապես ամեն ձկան մոտ դրվում էր մեկ դանակ։
Աշխարհում այսօր կիրառվում են երկու տեսակի թվագրություններ՝ արաբական և հռոմեական։
Հռոմեական թվերն ստեղծվել են ավելի քան 2000 տարի առաջ՝ Իտալիայում բնակվող էտրուսկ կոչվող հին ժողովրդի կողմից։ Հին Հռոմում թվերը գրում էին լատիներենի այբուբենի տառերի օգնությամբ։
Հռոմեական թվագրության մեջ կիրառվում են այս տառերը․ 1 — I (лат. unus), 5 — V (лат. quinque), 10 — X (лат. decem), 50 — L (лат. quinquaginta), 100 — (C лат. centum), 500 — (D лат. quingenti), 1000 — (M лат. mille)։ Հիշելով ռուսերեն այս նախադասություններըˋ “Мы Dарим Сочные Lимоны, Хватит Vсем Iх” կարելի է հիշել հռոմեական թվերը մեծից փոքրˋ Mˋ 1000, Dˋ 500, Cˋ 100, Lˋ 50, Xˋ 10, Vˋ 5, Iˋ 1:
Մյուս թվերը գրելու համար այս տառերի աջից կամ ձախից գրում էին տարբեր տառեր։ Եթե տվյալ տառին նախորդում էր մեկ այլ տառ, ապա այն փոքրացնում էր թիվը, իսկ եթե գրվում էր տառից հետո՝ թիվը մեծանում էր։ Օրինակ՝ V (5), եթե դիմացից ավելացնենք I տառը, կստանանք IV (4), իսկ եթե մյուս կողմից կցենք I տառը, կստանաք VI (6)։ Սիմվոլի վրա նշվող հորիղոնական մեկ գիծը նշանակում է դրա հազարապատիկը, իսկ երկու գիծը՝ միլիոնապատիկը։
Բնական թվերը գրելու համար թվանշանները կրկնում են։ Ընդ որում, եթե մեծ թիվը գրված է փոքրից առաջ, ապա նրանք գումարվում են, իսկ եթե փոքրն է մեծից առաջ, ուրեմն այն հանվում է մեծից։
Սակայն այսկերպ մաթեմատիկական հաշվարկներ կատարելը չափազանց բարդ է։ Այդ պատճառով հռոմեական թվագրումն այսօր օգտագործվում է միայն դարեր նշելու, հրատարակչություններում՝ գրքերի գլուծները նշելու մեջ, նաև ժամացույցների առանձին տեսակի թվատախտակների վրա։
1․ Փորձենք ընթերցել MMDCCCXXII թիվը։
1000 + 1000 + 500 + 100 + 100 + 100 + 10 + 10 + 1 + 1 = 2822.
Պատ․ 2822
2. Հռոմեական թվերով գրենք 2022
M+M+X+X+II= MMXXII
Պատ․ MMXXII
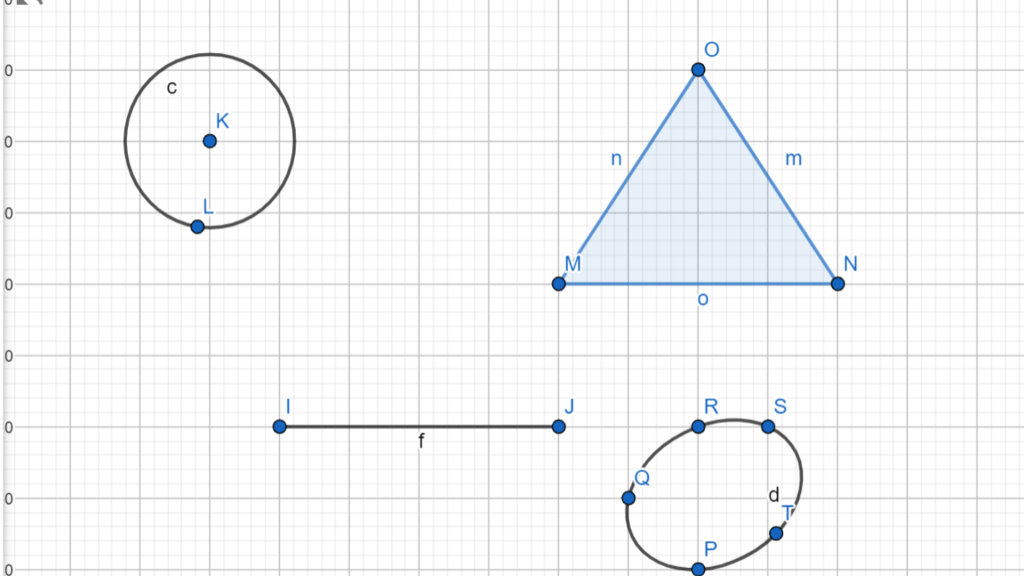
GeoGebra երկրաչափական ծրագրի յուրացում
Մաթեմատիկան՝ Ամանորին ընդառաջ
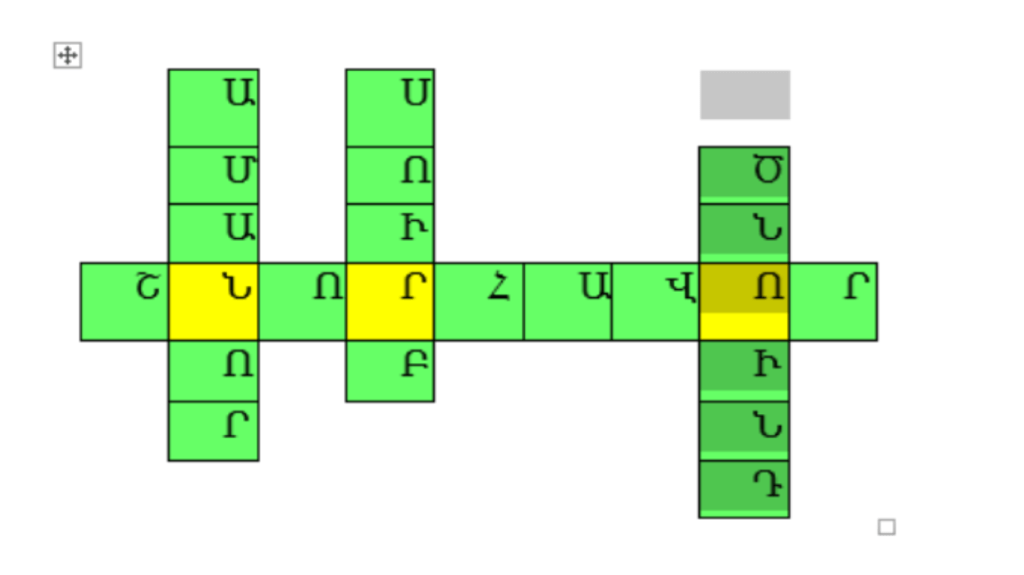
Թվերի գրառումը հայերենի այբուբենի տառերով․
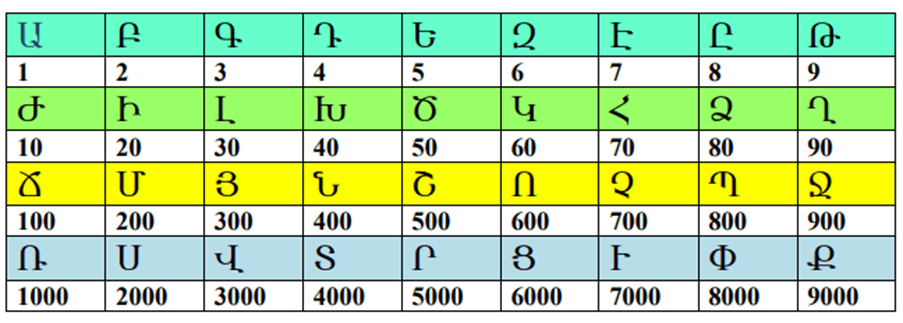
Հորիզոնական
- Գտե՛ք 500 և 25 թվերի ամենափոքր ընդհանուր բազմապատիկը։
500-Շ - Գտեք 40 թվի ամենամեծ բաժանարարի տասնապատիկը։
40×10=400-Ն - Գտե՛ք 600 և 2400 թվերի ամենամեծ ընդհանուր բաժանարարը։
600-Ո - Եթե Դավիթի մտապահած թվից հանեք 200, ստացած թիվը փոքրացնեք 2 անգամ կաստանաք 2400։
2400×2+200=500-Ր - Գտեք 6 թվի ամենամեծ և ամենափոքր բաժանարարների գումարի տասնապատիկը։
(6+1)x10=70-Հ - Բնական թվերից ո՞րն է ո՛չ պարզ, ո՛չ պաղադրյալ։
1-Ա - Գտե՛ք 3 և 1000 թվերի ամենափոքր ընդհանուր բազմապատիկը։
3000-Վ - Ո՞ր թիվն է մտապահել Անահիտը, եթե նրա մտապահած թվի և 256-ի տարբերությունը 344 է։
344+256=600-Ո - Գտի՛ր թիվը, որը 24-ի բաժանելիս ստացվում է 208 և 8 մնացորդ։
500-Ր
Ուղղաձիգ 1․
- Ո՞րն է ամենափոքր բնական թիվը։
1-Ա - Պարկում կա 95 կանաչ, 20 դեղին և 104 կարմիր գնդակ։ Առանց նայելու ամենաքիչը քանի՞ գնդակ պետք է հանել, որպեսզի դրանց մեջ լինեն տարբեր գույնի գնդակներ։
199+1=200-Մ - Գտեք ամենափոքր քառանիշ թվի և ամենամեծ եռանիշ թվի տարբերությունը։
- Ն
1000-999=1-Ա - Ո՞ր թիվն է մտապահել Նարեկը, եթե նրա մտապահած թվի կրկնապատիկի և 30-ի քանորդը 40 է։
(40×30):2=600-Ո - Գտեք 25 և 2 թվերի ամենափոքր ընդհանուր բազմապատիկի հարյուրապատիկը։
5000-Ր
Ուղղաձիգ 2․
- Ո՞ր թիվն է մտապահել Սոնան, եթե նրա մտապահած թվի 40 և 25 թվերի ամենափոքր ընդհանուր բազմապատիկի տասնապատիկն է։
2000-Ս - Գտեք 20-ի և 3-ի ամենափոքր ընդհանուր բազմապատիկի տասնապատիկը։
600-Ո - Գտեք ամենափոքր քառանիշ թվի և 7-ի ամենափոքր ընդհանուր բազմապատիկը։
- Ր
7000-Ւ - Ո՞րն է ամենափոքր պարզ թիվը։
2-Բ
Ուղղաձիգ 3․
- Ո՞րն է 100 և 150 թվերի ամենամեծ ընդհանուր բաժանարարը։
50-Ծ - Ավտոմեքենայի արագությունը 80կմ/ժ է։ Քանի՞ կիլոմետր կանցնի ավտոմեքենան 5 ժամում։
400-Ն - Ո
- Որքանո՞վ կմեծանա եռանիշ թիվը, եթե նրան ձախից կցագրենք 7 թվանշանը։
7000-Ւ - Ո՞րն է ամենափոքր եռանիշ թվի քառապատիկը։
400-Ն - Գտեք 3 թվի ամենամեծ և ամենափոքր բաժանարարների գումարը։
4-Դ