1) Գտե՛ք 3x — 4y + 5 = 0 ուղղի և կոորդինատային առանցքների հատման կետերի կոորդինատները:
x=0
-4y+5=0
y=5/4
(0;5/4)

y=0
3x+5=0
x=5/3
(5/3;0)
2) Գտե՛ք 2x — 3y + 1 = 0 և 3x + y — 4 = 0 ուղիղների հատման կետի կոորդինատները:
2x-3(4-3x)+1=0
2x-12+9x+1=0
11x-11=0
x=1
y=1
3) Գրե՛ք A(1; 3), B(2; -3) կետերով անցնող ուղղի հավասարումը:
x-1/2-1=y-3/-3-3
x-1/1=y-3/-6
-6x+6=y-3
-6x-y+3=0
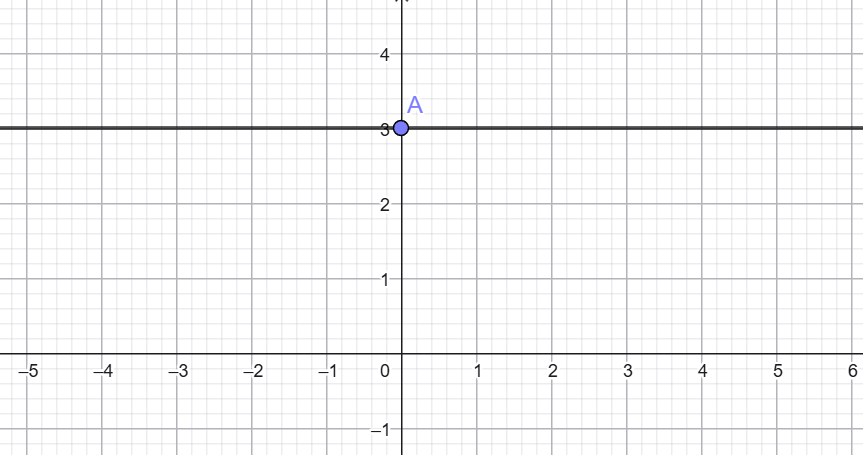
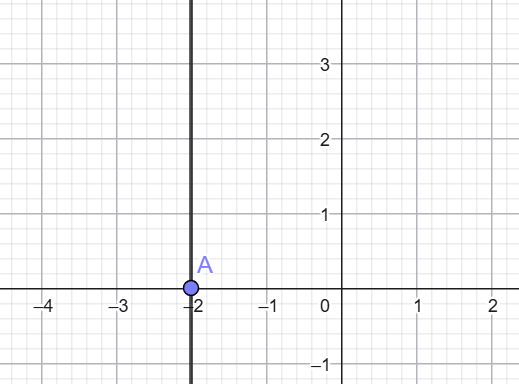
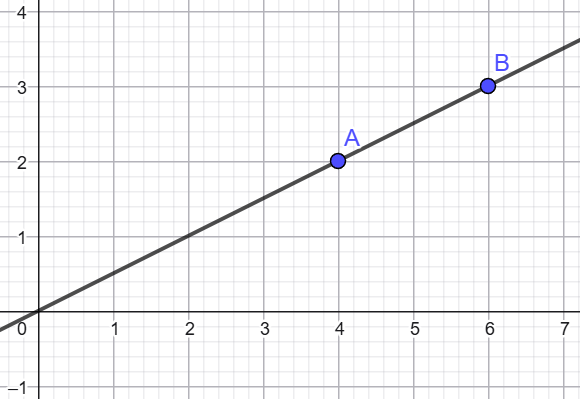
4) Գծագրեք այն ուղիղը, որը տրված է հետևյալ հավասարումով.
ա) y = 3

բ) x = — 2

գ) x — 2y = 0
(4;2), (6;3)

դ) 3x — y + 1 = 0

5) Գրե՛ք A(4; 6), B(-4; 0), C(-1; −4) գագաթներով ABC եռանկյան CM միջնագիծն
ընդգրկող ուղղի հավասարումը:
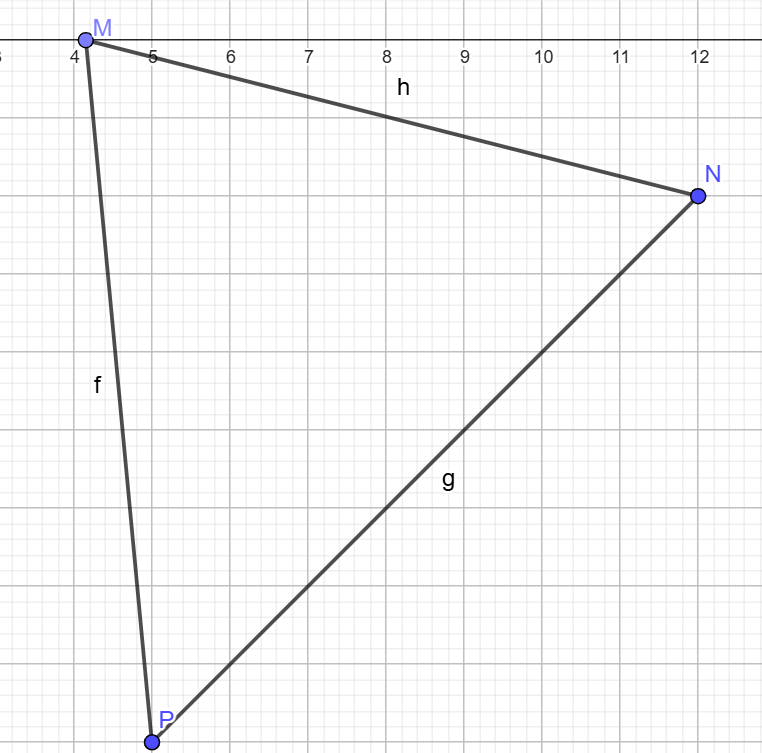
6) Գրեք M(4; 0), N(12; — 2), K(6; 8) գագաթներով MNK եռանկյան MK կողմին
զուգահեռ միջին գիծն ընդգրկող ուղղի հավասարումը:

Առաջադրանքներ․
1) Գրե՛ք կոորդինատների սկզբնակետով և M(3; 3) կետով անցնող ուղղի հավասարումը:
x=y
2) Գրե՛ք կոորդինատների սկզբնակետով և N(2; — 2) կետով անցնող ուղղի հավասարումը:
x=-y
3) Գրեք այն ուղղի հավասարումը, որն անցնում է տրված երկու կետերով․
ա) A(1; −1) և B(-3; 2)
x-1/-3-1=y+1/2+1
x-1/-4=y+1/3
3x-3=-4y-4
3x+4y+1=0
բ) C(2; 5) և D(5; 2)
x-2/5-2=y-5/2-5
x-2/3=y-5/-3
-3x+6=3y-15
-3x+3y+21=0
գ) M(0; 1) և N(-4; -5)
x-0/-4-0=y-1/-5-1
x/-4=y-1/-6
-6x+=-4y+4
-6x+4y+4=0
4) Գտեք 4x + 3y — 6 = 0 և 2x + y — 4 = 0 ուղիղների հատման կետի կոորդինատները։
{4x+3y-6=0
{6x+3y-12=0
2x-6=0
x=3, y=-2
5) Սեպտեմբեր ամսվա մաթեմատիկական ֆլեշմոբ․

1) Oxy հարթության վրա շրջանագիծը տրված է հետևյալ հավասարումով. Ինչի՞ են հավասար շրջանագծի կենտրոնի կոորդինատները և շառավիղը:
ա) x² +y² =36
O (0;0), R=6
բ) (x — 3)² + (y — 5)² = 25
O (3;5), R=5

2) Շրջանագիծը տրված է (x + 4)² + (y — 3)² = 2,56 հավասարումով: Նշե՛ք, թե (-4, 4), (-2, 1), (-2, 3), (-5, 4) կետերից որոնք են ընկած`
ա) շրջանագծի վրա
Ոչ մի կետ
բ) տրված շրջանագծով եզերված շրջանի ներսում
(-4;4)
գ) տրված շրջանագծով եզերված շրջանից դուրս
(-2;1), (-2;3)

3) Գրե՛ք r շառավիղով և O կենտրոնով շրջանագծի հավասարումը, եթե`
ա) r = 1, O(0, -7)
(x-0)²+(y-7)²=1²
բ) r = 5, O(1, -2)
(x-1)²+(y+2)²=5²
գ) r = 0,5, O(-3, -7)
(x+3)²+(y+7)²=0,5²

4) Գրե՛ք այն շրջանագծի հավասարումը, որի կենտրոնը կոորդինատների սկզբնակետն է, և որն անցնում է՝
ա) (1, 2)
(x-1)²+(y-2)²=5²
բ) (-3, 5)
(x+3)²+(y-5)²=34²
գ) (4, -3) կետով
(x-4)²+(y+3)²=23²

5) Գրե՛ք M կենտրոնով և N կետով անցնող շրջանագծի հավասարումը, եթե՝
ա) M(−1, 2), N(0, 5)
բ) M(0, 3), N(-2, 6)

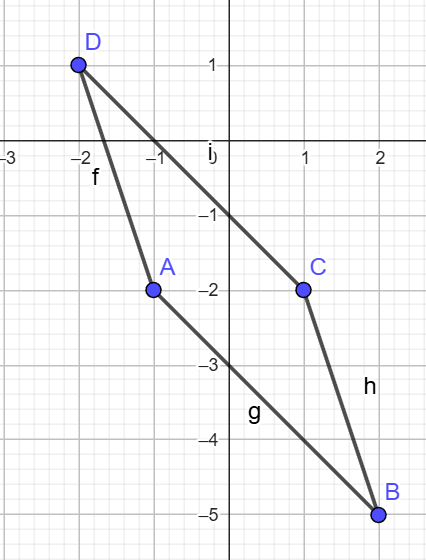
6) Գտե՛ք A(-1,-2), B(2, −5), C(1, -2), D(-2, 1) գագաթներով ABCD զուգահեռագծի պարագիծը և անկյունագծերը:
AB=√(2+1)²+(-5+2)²=√18
BC=√(1-2)²+(-2+5)²=√10
CD=√(-2-1)²+(1+2)²=√18
DA=√(-1+2)²+(-2-1)²=√10
P=(√18*2)+(√10*2)≈14,8

Առաջադրանքներ․
1) Գրե՛ք 7 շառավղով շրջանագծի հավասարումը, եթե դրա կենտրոնը կոորդինատների սկզբնակետն է:
R=7, (0;0)
x²+y²=49

2) Գրեք A(-2; 3) կենտրոնով շրջանագծի հավասարումը, որն անցնում է B(1; 2) կետով:
R
R=√(1-(-2))²+(2-3)²=√10
(x+2)²+(y-3)²=√10

3) Գտե՛ք O(3;1) կենտրոնով և A (6; -3) կետով անցնող շրջանագծի շառավիղը:
R=√(3-6)²+(1+3)²=√25=5

4) Ինչի՞ է հավասար (x — 11)² + (y + 24)² = 36 հավասարմամբ որոշվող շրջանագծի տրամագիծը:
6*2=12

5) Գրե՛ք A(2; — 1) կենտրոնով և R = 4 շառավղով շրջանագծի հավասարումը:
(x-2)²+(y+1)²=4²=16

6) A(2; 3), B(3; 4), C(5; 0), D(-4; 5), E(-3; 4) կետերից որոնք են գտնվում x²+ y² = 25 հավասարմամբ որոշվող շրջանագծի վրա:
B և E կետերը

7) Գրե՛ք AB տրամագծով շրջանագծի հավասարումը, եթե A(3; 5), B(7; 3):

Առաջադրանքներ․
1) Գտեք ABCD զուգահեռագծի D գագաթի կոորդինատները, եթե A(0, 0) B(5, 0) C(12,- 3):
D (7;-3)

2) Գտեք A և B կետերի հեռավորությունը, եթե`
ա) A(2, 7), B(-2, 7)
dAB=√(2-2)²+(7-7)²=√16=4
բ) A(-5, 1), B(-5, -7)
dAB=√(-5-5)²+(1-7)²=√136
գ) A(-3, 0), B(0, 4)
dAB=√(-3-0)²+(0-4)²=√25=5
դ) Α(0, 3), B(-4, 0)
dAB=√(0-4)²+(3-0)²=√25=5
3) Գտեք MNP եռանկյան պարագիծը, եթե M(4, 0), N(12, -2), P(5, -9):
dMN=√(4-12)²+(0-2)²=√68
dNP=√(12-5)²+(-2-9)²=√98
dPM=√(5-4)²+(-9-0)²=√82
P=√68+√98+√82

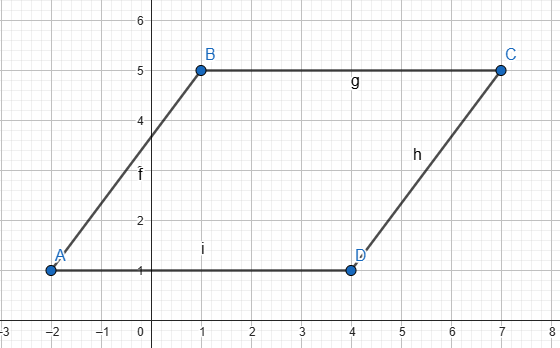
4) Տրված են A(-2;1), B(1;5), C(7;5), D(4;1) կետերը: Գտեք ABCD քառանկյան անկյունագծերը և պարագիծը:
dAB=√(-2-1)²+(1-5)²=√25=5
dBC=√(1-7)²+(5-5)²=√36=6
dCD=√(7-4)²+(5-1)²=√25=5
dDA=√(-2-4)²+(1-1)²=√36=6
P=5*2+6*2=22

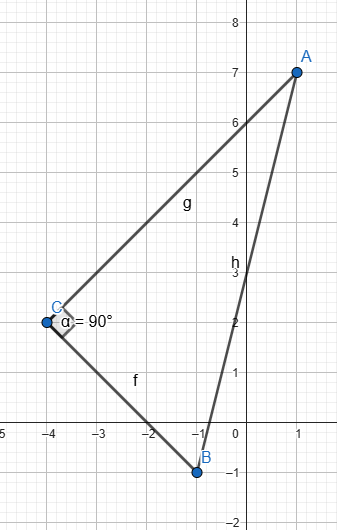
5) Ապացուցեք, որ A(1; 7), B(-1; -1), C(-4; 2) գագաթներով ABC եռանկյունը ուղղանկյուն եռանկյուն է: Գտե՛ք այդ եռանկյան ներքնաձիգին տարված միջնագիծը:

6) Գտե՛ք A(1; -2), B(3; 5), C(8; 0) գագաթներով ABC հավասարասրուն եռանկյան մակերեսը:

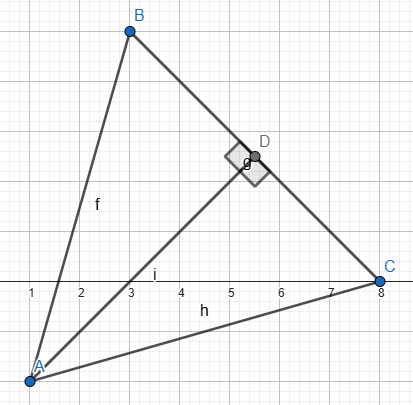
dAB=√(1-3)²+(5-2)²=√53
dBC=√(3-8)²+(5-0)²=√50
dCA=√(8-1)²+(0-2)²=√53
h²+√25²=√53²
h=√14
S=1/2*√50*√14=5√7

Առաջադրանքներ․
1) Գտե՛ք A և B ծայրակետերով հատվածի միջնակետի կոորդինատները, եթե
ա) A(2; 3), B(-2; 1)
x=2-2/2=0
y=3+1/2=2

D(0;2)
բ) A(1; 8), B(5; 5)
x=1+5/2=3
y=8+5/2=6,5

D(3;6,5)

2) Գտե՛ք AB հատվածի B ծայրակետի կոորդինատները, եթե C(2; — 1) կետը այդ հատվածի միջնակետն է, իսկ A ծայրակետը ունի (3; 5) կոորդինատները:
3+xB/2=2=3+xB=4
5+yB/2=-1=5+yB=-2
xB=1, yB=-7
B(1;-7)
3) Գտե՛ք B կետի կոորդինատները, եթե այն A(3; −4) կետի համաչափն է կոորդինատների սկզբնակետի նկատմամբ:
B(-3;4)

4) Գտե՛ք A(-2; 3) կետի` x-երի առանցքի նկատմամբ համաչափ B
կետի կոորդինատները:
B(-2;-3)

5) Գտե՛ք C(7; 2) կետի՝ y-ների առանցքի նկատմամբ համաչափ D
կետի կոորդինատները:
D(-7;2)

6) Ինչի՞ է հավասար A(2; — 3) կետի հեռավորությունը՝
ա) x-երի առանցքից
3-ով
բ) y-ների առանցքից
2-ով
գ) կոորդինատների սկզբնակետից
√(2-0)²+(-3-0)²=√13

7) Գտե՛ք A և B կետերի հեռավորությունը, եթե.
ա) A(1;-3), B(1; 2)
5
բ) A(2; 3), B(1; −1)
4
գ) A(0; 2), B(4; -1)
3

8) Գտեք ABC եռանկյան պարագիծը, եթե A(8; 1), B(5; -3), C(11; -3)։

9)Գտեք Ox առանցքի այն կետի կոորդինատները, որը գտնվում է A(5;3) կետից 5 հեռավորության վրա: