1) Գտե՛ք sinɑ -ն, եթե.
ա) cosɑ = 0
sinɑ=1
բ) cosɑ = — 1/2
sinɑ=√3/2
գ)cosɑ = √3/2
sinɑ=-1/2
դ)cosɑ = — 1
sinɑ=2

2) Գտեք sinɑ -ն ու ctgɑ -ն, եթե
ա) cosɑ = -√3/2
sinɑ=1/2
ctgɑ=1/√3
բ) cosɑ = -√2/2
sinɑ=
ctgɑ=

3) Գտեք cosɑ–ն, եթե՝
ա) sinɑ = √3/2
cosɑ=1/2
բ) sinɑ = 1/4

գ) sinɑ=0
cosɑ=1

4) Գտե՛ք արտահայտության արժեքը.

ա) sin108^o/sin72^o=1
բ) cos17^o/cos163^o=-1
գ) tg42^o/tg138^o=-1

Առաջադրանքներ․

1)

ա) դրակա
բ) բացասական
գ) զրո

2)

ա) դրակա
բ) բացասական
գ) զրո

3)

ա) +
բ) —
գ) +
դ) —

4)

ա) cosα
բ) sinα
գ) cosα
դ) -sinα

5)

sin120^o=√3/2
cos120^o=-√3/2
tg120^o=-1
ctg120^o=-1

6)

sin135^o=√2/2
cos135^o=-√2/2
tg135^o=-1
ctg135^o=-1

7)

sin150^o=1/2
cos150^o=-1/2
tg150^o=-1
ctg150^o=-1

1) Շրջանագծի հատողն իր արտաքին մասից մեծ է 2.1/4 անգամ։ Հատողը նույն կետից տարված շոշափողից քանի՞ անգամ է մեծ։
AD/AB
AD=2.25x
AB²=x*2.25x=2.25x²
AB=1.5x
2.25x/1.5x=1.5
2) Դիցուք՝ AB-ն շոշափող է, AD-ն՝ նույն շրջանագծի հատող, որի արտաքին մասը AC-ն է։ Որոշեք՝
ա) CD-ն, եթե AB = 2 սմ և AD = 4 սմ
AB²=AC*AD
AC=AB²/AD=4/4=1
CD=AD-AC=4-1=3
բ) AD-ն, եթե AC : CD = 4/5 և AB = 12 սմ
AC=4, CD=5
AB²=AC*AD
AD=AB²/AC=144/4=36
3) Մի կետից շրջանագծին տարված շոշափողն ու հատողը համապատասխանաբար հավասար են 20 սմ և 40 սմ, իսկ հատողի հեռավորությունը շրջանագծի կենտրոնից՝ 8 սմ։ Գտեք շրջանագծի շառավիղը։
400=40*40-2x
40-2x=10
2x=30x
x=15
8²+15²=225
√225=15
4) Մի կետից շրջանագծին տարված են հատող և շոշափող: Որոշեք շոշափողի երկարությունը, եթե նա հատողի արտաքին մասից 5 սմ–ով մեծ է, իսկ ներքին մասից` նույնքանով փոքր:
5) Մի կետից նույն շրջանագծին տարված են երկու հատող՝ որոնց երկարություններն են 15 սմ և 25 սմ։ Գտեք նրանց արտաքին մասերը, եթե հայտնի է, որ դրանցից մեկը 2 սմ–ով մեծ է մյուսից։
AC₁=15
AC₂=25
AB₁*AC₁=AB₂*AC₂
15(x+2)=25x
15x+30=25x
10x=30
x=3
3+2=5

Առաջադրանքներ․
Խնդիրների պայմաններում C ուղիղ անկյունով և CH բարձրությունով ABC ուղղանկյուն եռանկյան տարրերի համար օգտագործված են հետևյալ նշանակումները. BC = a, AB = c, AC = b, CH = h, AH = b_c, BH = a_c :
1) Գտեք՝
ա) h–ը, a–ն և b–ն, եթե b_c = 25 , a_c = 16
AB=c=16+25=41
h=√a_c*b_c=√16*25=20
b²=h²+b_c²=400+625=1025
b=√1025=32
a²=h²+a_c²=400+256=656
a=√656=25.6
բ) h — ը, a–ն և b-ն, եթե b_c = 36, a_c = 64
AB=c=36+64=100
h=√a_c*b_c=√64*36=48
b²=h²+b_c²=2304+1296
b=√3600=60
a²=h²+a_c²=2304+4096
a=√6400=80
գ) a-ն, c-ն և a_c — ն, եթե b = 12, b_c = 6
h²+6²=12²
h²=144-36=108
h=√108=10.3
h²=a_c*b_c
108=a_c*6
a_c=108/6=18
c=a_c+b_c=18+6=24
a²+144=576
a²=576-144=432
a=√432=20.7
դ) b-ն, c-ն և b_c — ն, եթե a = 8, a_c = 4
h²+16=64
h²=64-16=48
h=√48=6.9
h²=a_c*b_c
48=4*b_c
b_c=48/4=12
c=a_c+b_c=12+4=16
b²+64=256
b²=256-64=192
a=√192=13.8
ե) h–ը, b–ն, a_c — ն և b_c — ն եթե a = 6, c = 9
2) Ուղղանկյուն եռանկյան էջերը հարաբերում են, ինչպես 3 : 4, իսկ ներքնաձիգը հավասար է 50 մմ։ Գտեք այն հատվածները, որոնց տրոհվում է ներքնաձիգը ուղիղ անկյան գագաթից տարված բարձրությունով։
a/3x=50-a/4x
4a=150-3a
7a=150
a=150/7
3) BD հատվածը ABC եռանկյան կիսորդն է։
ա) Գտեք AB–ն, եթե BC = 9սմ, AD = 7,5 սմ, DC = 4,5 սմ։
BC/DC=AB/AD
9/4.5=AB/7.5
AB=15
բ) Գտեք DC–ն, եթե AB = 30 սմ, AD = 20սմ, BD = 16սմ և <BDC = <C։
20/30=DC/16
DC=16*20/30=32/3
4) AD հատվածը ABC եռանկյան կիսորդն է։ Գտեք BD–ն և DC–ն, եթե AB = 14 սմ, BC = 20 սմ, AC = 21 սմ։
14/x=21/20-x
280-14x=21x
35x=280
x=8

Առաջադրանքներ․
1) AB և CD հատվածները հատվում են M կետում այնպես, որ MA = 7 սմ, MB = 21 սմ, MC = 3 սմ և MD = 16 սմ: A, B, C և D կետերը գտնվու՞մ են, արդյոք, միևնույն շրջանագծի վրա։
3*16=48
7*21=147
Ոչ, չեմ գտնվում միևնույն շրջանագծի վրա
2) Շրջանագծի երկու լարեր հատվում են: Մի լարի հատվածները հավասար են 24 սմ և 14 սմ, իսկ մյուս լարի հատվածներից մեկը`28 սմ: Գտեք երկրորդ լարի երկարությունը:
24*14=336
336/28=12
3) Երկու իրար հատող լարերից մեկը տրոհված է 48 մ և 3 մ հատվածների, իսկ մյուսը` կիսվում է։ Որոշեք երկրորդ լարի երկարությունը։
x*x=3*48
x²=144
x=√144=12
12+12=24
4) Երկու իրար հատող լարերից մեկը տրոհված է 12 մ և 18 մ հատվածների, իսկ երկրորդը` 3 : 8 հարաբերությամբ։ Որոշեք երկրորդ լարի երկարությունը։
12*18=3x*8x
24x=216
x<sup>2</sup>=216/24=9
x=3
3*3=9
8*3=24
5) Իրար հատող երկու լարերից առաջինը 32 սմ է, իսկ երկրորդ լարի հատվածներն են 12 սմ և 16 սմ: Որոշեք առաջին լարի հատվածները։
12*16=x(32-x)
x<sup>2</sup>-32x+192=0
D=1024-768=256
x1=32+16/2=24
x2=32-16/2=8
6) Մի կետից շրջանագծին տարված են հատող և շոշափող: Որոշել շոշափողի երկարությունը, եթե հատողի արտաքին և ներքին մասերի երկարությունները համապատասխանաբար հավասար են՝
ա) 4 սմ և 5 սմ
4*(4+5)=36
√36=6
բ) 2,25 դմ և 1,75 դմ
2.25*(2.25+1.75)=9
√9=3
գ) 1 մ և 2 մ։
1*(1+2)=3
√3=1.7
7) Շոշափողը 20 սմ է, իսկ նույն կետից տարված և շրջանագծի կենտրոնով անցնող հատողը` 50 սմ։ Գտեք շրջանագծի շառավիղը։
400=50*(50-2R)
400/50=8
50-8=2R=42
R=21

Առաջադրանքներ․
1) O-ն ABC եռանկյան միջնագծերի հատման կետն է: Գտե՛ք AO հատվածի երկարությունը, եթե AK միջնագիծը 18 դմ է:
18/3=6
AO=6*2=12
OK=6
2) O-ն ABC եռանկյան միջնագծերի հատման կետն է: Գտե՛ք AK միջնագծի երկարությունը, եթե OK-ն 5 սմ է:
AO=5*2=10
AK=10*5=50
3) Տարված է C ուղիղ անկյունով ABC եռանկյան CH բարձրությունը: Գտե՛ք AB ներքնաձիգը, եթե AC = 6 սմ, AH = 3 սմ:
6²/3=12
4) Ուղղանկյուն եռանկյան ներքնաձիգին տարված բարձրությունը այն բաժանում է 4 սմ և 5 սմ երկարությամբ հատվածների: Գտե՛ք եռանկյան էջերը:
AC²=5*9=45
BC²=4*9=36
AC=√45
BC=√36
5) Տարված է C ուղիղ անկյունով ABC եռանկյան CH բարձրությունը:
Գտեք AB ներքնաձիգը, եթե AH:HB=4:5, AC = 6 դմ:
AC²=AH*AB
AH=4k
HB=5k
AB=AH+HB=4+5=9
6²=36=4k*9k=36k²
AB=9k=9
6) Ուղղանկյուն եռանկյան ներքնաձիգին տարված բարձրությունն այն բաժանում է 9 սմ և 16 սմ երկարությամբ հատվածների: Գտե՛ք այդ եռանկյան պարագիծը:

1) ABC և A₁B₁C₁ եռանկյունները նման են, ընդ որում՝ k = 3 : Գտեք ABC եռանկյան մակերեսը, եթե A₁B₁C₁ եռանկյան մակերեսը 16 սմ² է:
S_ABC/S_A1B1C1=k²
S_ABC=16*9=144
144/16=9
2) Նման եռանկյուններից մեկի մակերեսը 20 դմ² է, մյուսինը`5 դմ²: Գտե՛ք այդ եռանկյունների նմանության գործակիցը:
400/25=16
k=√16=4
3) Նման եռանկյուններից մեկի կողմը 24 սմ է, իսկ մյուս եռանկյան դրան նմանակ կողմը 6 սմ է: Գտեք երկրորդ եռանկյան մակերեսը, եթե առաջինի մակերեսը 160 սմ է:
k=24/6=4
160/4²=10
4) Նման եռանկյուններից մեկի կողմերը 5 անգամ փոքր են մյուսի կողմերից: Գտե՛ք դրանց մակերեսների հարաբերությունը:
k=5²
5) M-ը ABCD զուգահեռագծի BC կողմը բաժանվում է 1:2 հարաբերությամբ՝ հաշված B կետից: AM և BD հատվածները հատվում են K կետում: Գտե՛ք K կետի հեռավորությունը AD-ից, եթե K կետի հեռավորությունը BC-ից 5 սմ է։
6) BC = 6 սմ և AD = 18 սմ հիմքերով ABCD սեղանի անկյունագծերը հատվում են O կետում: Գտե՛ք AOD եռանկյան OM միջնագիծը, եթե BOC եռանկյան OK միջնագիծը 8 սմ է:
k=18/6=3
8*3=24
7) BC = 4 սմ և AD = 8 սմ հիմքերով ABCD սեղանի անկյունագծերը հատվում են O կետում: M-ը և N–ը համապատասխանաբար AO և OC հատվածների միջնակետերն են: Գտե՛ք DM-ը, եթե BN = 3 սմ:

Առաջադրանքներ․
1) ABC և A₁B₁C₁ եռանկյունները նման են, ընդ որում՝ k = 4 : Գտեք ABC եռանկյան պարագիծը, եթե A₁B₁C₁ եռանկյան պարագիծը 26 դմ է:
26*4=104
2) Նման եռանկյուններից մեկի պարագիծը 28 սմ է, մյուսինը՝ 7 սմ: Գտե՛ք այդ եռանկյունների նմանության գործակիցը:
k=28/7=4
3) Նման եռանկյուններից մեկի կողմը 32 սմ է, մյուս եռանկյան դրան նմանակ կողմը 8 սմ է: Գտե՛ք երկրորդ եռանկյան պարագիծը, եթե առաջինի պարագիծը 120 սմ է։
k=32/8=4
120/4=30
4) Նման եռանկյուններից մեկի կողմերը 6 անգամ փոքր են մյուսի կողմերից: Գտե՛ք դրանց պարագծերի հարաբերությունը:
6
5) ABC և A₁B₁C₁ եռանկյունները նման են, ընդ որում՝ ∠A = ∠A₁, ∠B = ∠B₁: BM-ը և B₁M₁-ը այդ եռանկյունների միջնագծերն են: Գտե՛ք B₁M₁-ը, եթե AB = 12 սմ, A₁B₁ = 4 սմ, BM = 9 սմ։
k=12/4=3
B₁M₁=9/3=3
6) ABC և A₁B₁C₁ եռանկյունները նման են, ընդ որում՝ ∠A = ∠A1, ∠B = ∠B₁: AK-ն և A₁K₁-ը այդ եռանկյունների կիսորդներն են: Գտե՛ք BC-ն, եթե AK = 9 սմ, A₁K₁ = 3 սմ, B₁C₁ = 7 սմ:
k=9/3=3
BC=3*7=21
7) ABC և A₁B₁C₁ եռանկյունները նման են, ընդ որում՝ ∠A = ∠A₁, ∠B = ∠B₁: BH-ը և B₁H₁-ը այդ եռանկյունների բարձրություններն են: Գտե՛ք AC-ն, եթե BH =15 սմ, B₁H₁ = 6 սմ, A₁C₁ = 8 սմ։
k=15/6=2.5
AC=2.5*8=20

1) Ապացուցեք, որ նկարում պատկերված եռանկյունները նման են։

4.5/3=1.5
6/4=1.5
9/6=1.5
Հետևաբար՝ ըստ եռանկյունների նմանության երրորդ հայտանիշի՝ եթե մի եռանկյան երեք կողմերը համեմատական են մյուս եռանկյան երեք կողմերին, ապա եռանկյունները նման են:

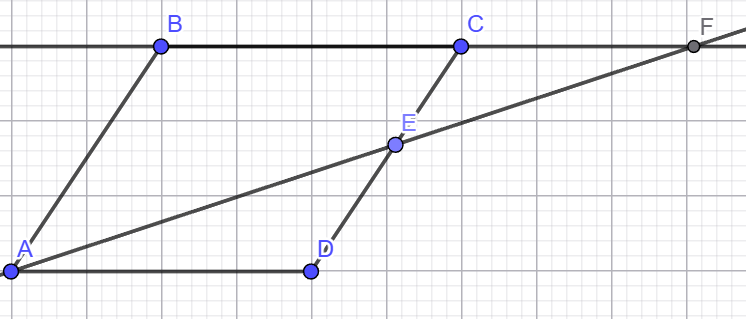
2) ABCD զուգահեռագծի CD կողմի վրա նշված է E կետը: AE և BC ուղիղները հատվում են F կետում։ Գտեք`
ա) EF–ը և FC-ն, եթե DE = 8 uմ, EC = 4 սմ, BC = 7 սմ, AE = 10 սմ,
EF/AE=EC/DE
EF=4*10/8=5
FC/AD=7/2
FC=3.5
բ) DE–ն և EC-ն, եթե AB = 8 սմ, AD = 5 սմ, CF = 2 սմ:

3) AB և CD հիմքերով ABCD սեղանի անկյունագծերը հատվում են O կետում։ Գտեք`
ա) AB–ն, եթե OB = 4սմ, OD = 10 սմ, DC = 25 սմ,
բ) (AO)/(OC)-ն և (BO)/(OD) -ն եթե AB = a, DC = b
գ) AO-ն, եթե AB = 9,6 դմ, DC = 24 սմ, AC = 15 սմ:
4) ABC եռանկյան AB կողմը 15 սմ է, իսկ AC կողմը` 20 սմ։ AB կողմի վրա անջատված է AD = 8 սմ, իսկ AC կողմի վրա՝ AE = 6 սմ հատվածը։ Նման են, արդյոք, ABC և ADE եռանկյունները
15/8≠20/6
Ոչ, նման չեն
5) Նման են, արդյոք, երկու ուղղանկյուն եռանկյունները, եթե դրանցից մեկն ունի 40°–ի անկյուն, իսկ մյուսը`
ա) 50°–ին հավասար անկյուն
180-(40+50)=90 — այո
բ) 60°–ին հավասար անկյուն
180-(40+60)=80 — ոչ
6) Նման են, արդյոք, ABC և A<sub>1</sub>B<sub>1</sub>C<sub>1</sub> եռանկյունները, եթե`
ա) AB = 3սմ, BC = 5սմ, CA = 7սմ, A₁B₁ = 4,5սմ, B₁C₁ = 7,5սմ, C₁A₁ = 10,5սմ
3/4.5=5/7.5=7/10.5 — այո
բ)AB = 1,7սմ, BC = 3սմ, CA = 4,2սմ, A₁B₁ = 34դմ, B₁C₁ = 60դմ, C₁A₁ = 84դմ:
340/1.7=600/3=840/4.2 — այո

Առաջադրանքներ․
1) Նման են ABC և A₁B₁C₁ եռանկյունները, եթե AB = 3մ, BC = 4մ, AC = 6մ, A₁B₁ = 9մ, B₁C₁ = 12մ , A₁C₁ = 18մ:
Այո, եթե մի եռանկյան երեք կողմերը համեմատական են մյուս եռանկյան երեք կողմերին, ապա եռանկյունները նման են:
2) Նման են երկու եռանկյուններ, եթե մեկի կողմերը հարաբերում են ինչպես 3:8:9, իսկ մյուսի կողմերը 24 սմ, 9 սմ, 27 սմ են:
3*3=9
3*8=24
3*9=27
3) ABC և BCD եռանկյուններում AB = 36 սմ, BC = 18սմ, AC = 20 սմ, DC = 9սմ, DB = 10 սմ: Ապացուցեք, որ ΔABC ~ ΔBCD :
Այո, նման են։ Եթե մի եռանկյան երկու կողմերը համեմատական են մյուս եռանկյան երկու կողմերին, իսկ այդ կողմերով կազմված անկյունները հավասար են, ապա եռանկյունները նման են։
4) O գագաթով անկյան կողմերից մեկի վրա վերցված են A և B, իսկ մյուսի վրա C և D կետերը այնպես, որ AO = 4 սմ, BO = 7սմ, OC =12 սմ, OD = 21սմ: Նման են OAC և OBD եռանկյունները:
Այո, նման են։
5) Ըստ նկարների տվյալների՝ գտեք x–ը և y–ը։

6) M-ը և N-ը ABC եռանկյան համապատասխանաբար AB և BC կողմերի միջնակետերն են: Ապացուցեք, որ ABC եռանկյունը նման է MBN եռանկյանը: