Հանրահաշիվ՝
Թվային անհավասարությունների հատկությունները
Առաջին աստիճանի մեկ անհայտով անհավասարումներ
Միջակայքերի պատկերումը թվային ուղղի վրա
Առաջին աստիճանի մեկ անհայտով անհավասարումներ
Մեկ անհայտով գծային անհավասարումներ
Մեկ անհայտով գծային անհավասարումների համակարգեր
Մեկ անհայտով գծային անհավասարումների համախմբեր
Թվաբանական քառակուսի արմատ
Թվաբանական քառակուսի արմատ

Երկրաչափություն՝
Շրջանագծի աղեղի աստիճանային չափը
Եռանկյանը ներգծյալ և արտագծյալ շրջանագծեր
Եռանկյանը ներգծյալ և արտագծյալ շրջանագծեր
Քառանկյան ներգծյալ և արտագծյալ շրջանագիծ
Քառանկյան ներգծյալ և արտագծյալ շրջանագիծ
Երկու շրջանագծերի փոխադարձ դասավորությունը
Քառակուսու և ուղղանկյան մակերեսը
Քառակուսու և ուղղանկյան մակերեսը
Քառակուսու և ուղղանկյան մակերեսը
Զուգահեռագծի և շեղանկյան մակերեսը
Զուգահեռագծի և շեղանկյան մակերեսը
Եռանկյան մակերեսը

1) Գտե՛ք թիվ, որի քառակուսին հավասար է՝
ա) 4 — 2
բ) 100 — 10
գ) -6 — չկա
դ) 81 — 9
ե) -0,25 — չկա
զ) 0 — 0
է) 0,09 — 0,3
ը) 1,21 — 1,1

2) Հաշվե՛ք․
ա) 2 + √1=3
բ) 15 — √36=9
գ) √9 + √4=5
դ) √16 + √25=9
ե) √49 — √1=6
զ) √81 — √49=2
է) √100 — √36=4
ը) √144 — √121=1
թ) √0,36 + √0,49=1,3

3) Հաշվե՛ք․
ա) 2 • √81=18
բ) 1/3 • √100=10/3
գ) √4 • √0,25=1
դ) √0,16 • √9=1,2
ե) √0,27 : √3=0,3
զ) √49 : √0,01=70
է) √1/9 • √81=3
ը) √0,36 : √1/36=3,6
թ) √1,69 : √0,0625=5,2

4) Հաշվե՛ք․
ա) (√2)² =2
բ) (√3)² =3
գ) (√13)² =13
դ) (√17)² =17

5) Հաշվե՛ք․
ա)

7/9

բ)

8/10

գ)

4/3

դ)

3/2

ե)

13/29

6) Համեմատե՛ք թվերը․
ա) √100 և √81
10 > 9
բ) √100 և √121
10 < 11
գ) √4 և 3
2 < 3
դ) 1/5 և √0,25
0,2 < 0,5
ե) 2 և √1/16
2 > 0,25
զ) 9/5 և √4/49
1,8 > 0,04
է) √0,09 և √4/25
0,3 < 0,4
ը) √1/4 և 1/4
0,5 < 0,25

Առաջադրանքներ․
1) Արդյո՞ք նշված արտահայտությունն իմաստ ունի.

ա) այո
բ) այո
գ) ոչ
դ) այո
ե) ոչ
զ) այո
է) այո
ը) այո
թ) ոչ
ժ) ոչ

2) Գտե՛ք տրված կողմի երկարությամբ քառակուսու մակերեսը: Հարմարության համար կարելի է փոխել չափման միավորը.
ա) 3 մ
S=3²=9մ²
բ) 9 կմ
S=9²=81կմ²
գ) 0.05 կմ
S=0,05²=0,0025կմ²
դ) 2.8 սմ
S=2,8²=7,84սմ²
ե) 200 սմ
S=200²=40000սմ²
զ) 6000 մմ
S=6000²=36000000մմ²
է) 80 դմ
S=80²=6400դմ²
ը) 0.9մ
S=0,9²=0,81մ²
թ) 1.3 սմ
S=1,3²=1,69սմ²
ժ) 0.000003 կմ
S=0,000003²=0,000009կմ²

3) Թիվը բարձրացրե՛ք քառակուսի.

ա) 1²=1
բ) 7²=49
գ) 1,2²=1,44
դ) 0,1²=0,01
ե) √5²=5
զ) √1,222²=1,222
է) √14²=14
ը) 0²=0
թ) (-4,2)²=-17,64
ժ) —√6,8²=-6,8

4) Գտե՛ք քառակուսու կողմի երկարությունը, եթե նրա մակերեսը հավասար է.
ա) 25 մ²=√25=5
բ) 100 մմ²=√100=10
գ) 49 մ²=√49=7
դ) 0.01 սմ²=√0,01=0,1
ե) 64 դմ²=√64=8
զ) 0.09 սմ²=√0,09=0,3
է) 2.56 մ²=√2,56=1,6
ը) 10000 սմ²=√10000=100
թ) 144 սմ²=√144=12
ժ) 1.69 կմ²=√1,69=1,3

5) Հաշվե՛ք արտահայտության արժեքը.

ա) √4=2
բ) √25=5
գ) √16=4
դ) —√1=-1
ե) √0,01=0,1
զ) √100=10
է) √10000=100
ը) √441=21
թ) —√144=-12
ժ) √1000000=1000

Առաջադրանքներ․
1) Թվային բազմությունները պատկերե՛ք կոորդինատային առանցքի վրա և գտե՛ք նրանց միավորումը:
ա) [- 4, 11] և (- 7, 4]
[-7;11]
բ) (- 21, 0) և [- 14, 0]
[-21;0]
գ) (- ∞, 3) և [0, ∞)
[-∞;∞]
դ) (- 2, 6] և (8, 14)
(- 2, 6] U (8, 14)
ե) (- 9, 3.6) և [3.6, 9)
[-9;9]
զ) [- 15, -5] և [-4.5; 4]
[- 15, -5] U [-4.5; 4]
է) (- 9.2, -1.2] և (0, 5)
(- 9.2, -1.2] U (0, 5)
ը) [- 0.5, 3.7] և [3.7, 32)
[-0,5;32]
թ) (0, 0.1] և (- ∞, ∞)
[-∞;∞]

2) Արդյո՞ք -1 թիվը համախմբի լուծում է.

[-1+7>-2
[-3-2<23
Այո

[5+4<2+1
[-2,4-1<-3
Ոչ

[3,2+4>-1-10
[2+1>4*2
Այո

[1+3>-1-1
[8-5<20-6
Այո

[16+1<10+0,7
[-2*3>42
Ոչ

[-16-3>-12-1
[4-1>25+6
Ոչ

3) Լուծե՛ք համախումբը.

x∈(-2;∞)

y∈(0;-∞)

a∈(21;-∞)

z∈(1,6;∞)

Առաջադրանքներ․
1) Կոորդինատային ուղղի վրա նշեք անհավասարումների համակարգի բոլոր լուծումները (եթե դրանք գոյություն ունեն)․

x∈(3;∞)

x∈(1;∞)

x∈(-∞;2)

x∈(-∞;-5)

x∈(-7;-5)

x∈(-5;0)

x∈(4;∞)

x∈(-3;∞)

x∈(-∞;-1)

x∈(-16;-∞)

Լուծում չկա

2) Փակագծերում նշված թիվը հանդիսանո՞ւմ է արդյոք անհավասարումների համակարգի լուծում՝

{-2+3>0
{7+4>0
Այո

{8-2<0
{6≥3
Ոչ

{15>10
{18+1<0
Ոչ

Առաջադրանքներ․
1) Փակագծերում նշված թիվը հանդիսանո՞ւմ է արդյոք անհավասարման լուծում՝
4x-4>3x+3 (-1) — ոչ
-8>0
72x-18<-13x (-10) — այո
-738<130
2) Համարժե՞ք են արդյոք անհավասարումները՝
2x-1>6 և 6>2x-1 — ոչ
x<3 և x+2<5 — այո
3x-7>5 և -3x+7<-5 — ոչ
3) Լուծեք անհավասարումը`
2x+1<x
x < -1
x∈(-∞;-1)

7x-13>9x
-2x > 13
x<-6,5
x∈(-∞;-6,5)

2x-x-1<2
x < 3
x∈(-∞;3)

8-9x>x-3-3x+4x+15
-11x > 4
x < -4/11
x∈(-∞;-4/11)
4) Փակագծերում նշված թիվը հանդիսանո՞ւմ է արդյոք անհավասարման լուծում՝
2+12x<-x+3 (-2) — այո
-22<5
5x-7>9+x (100) — այո
493>109
5) Համարժե՞ք են արդյոք անհավասարումները՝
2x>4 և x<2 — ոչ
2x>5 և x-7>-2-x — այո
2<7-x և 3x<5+2x — այո
6) Լուծեք անհավասարումը`
x+4>5x
x < 1
x∈(-∞;1)

x-2<3x
x > -1
x∈(-∞;-1)

3<7x-5-4x
x > 8/3
x∈(-∞;8/3)

1) Լուծեք անհավասարումը․
ա) 2x > 4
x>2
x∈(2;∞)

բ) 7x < -14
x < -2
x∈(-∞;-2)

գ) -5x < 100
x > -20
x∈(-20;∞)

դ) -3x < 9
x > 3
x∈(3;∞)

ե) -2x > -2
x < 1
x∈(-∞;1)

զ) -3x > -6
x < 2
x∈(-∞;2)

է) 3x < 2
x < 2/3
x∈(-∞;2/3)

ը) -2x < 11
x > -5,5
x∈(-5,5;∞)

թ) -5x > 1
x < -5
x∈(-∞;-5)

ժ) -17x > -2
x < 8,5
x∈(-∞;8,5)

ի) -4x > -2
x < 2
x∈(-∞;2)

լ) 13x < 3
x < 3/13
x∈(-∞;3/13)

2) Լուծեք անհավասարումը․
ա) x — 1 > 0
x > 1
x∈(1;∞)

բ) 3 + x > 0
x > 3
x∈(3;∞)

գ) x + 5 < 0
x < 5
x∈(-∞;5)

դ) x + 0, 5 < 0
x < 0,5
x∈(-∞;0,5)

ե) x -1 1/3 < 0
զ) x — 6 < 6
x < 6
x∈(-∞;6)

է) x + 7 > 7
x > 7
x∈(7;∞)

ը) 3 + x < -6
x < -9
x∈(-∞;-9)

թ) x — 2 > 0, 6
x > 2,6
x∈(-∞;2,6)

ժ) x — 3, 5 < 4
ի) 7 + x > 0
x > 7
x∈(7;∞)

լ) 4 + x > 2
խ) x -11 < -7
ծ) x + 4 > 7
կ) x -2 > 0, 2
հ) x + 10, 7 > 7, 9
ձ) 2, 1 + x < 7
ղ) 5013 + x < 0 ,13

Առաջադրանքներ․
1) Անվանեք թվային բազմությանը պատկանող բոլոր ամբողջ թվերը՝
ա)[-3;1] — -3, -2, -1, 0, 1
բ)(-3;1) — -2, -1, 0
գ)[-3;1) — -3, -2, -1, 0
դ)(-3;1] — -2, -1, 0, 1
ե)[-2;3] — -2, -1, 0, 1, 2, 3
զ)(-2;3) — -1, 0, 1, 2
է)[-2;3) — -2, -1, 0, 1, 2
ը)(-2;3] — -1, 0, 1, 2, 3

2) Պատկերեք նշված բազմությունները թվային ուղղի վրա՝
ա)[3;5]

բ)(3;5)

գ)[3;5)

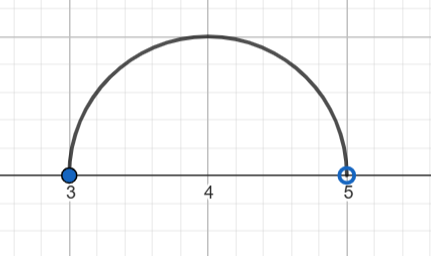
դ)(3;5]

ե)[-2;+∞)

զ)(-2;+∞)

է)(-∞;-2)

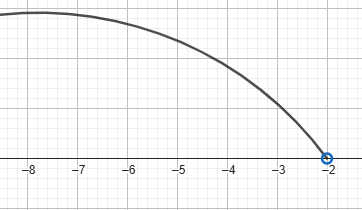
ը)(-∞;-2]

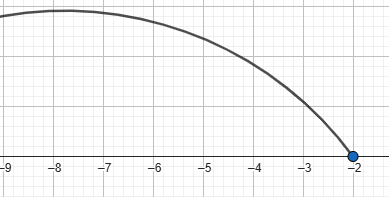
3) Պատկանու՞մ է արդյոք -2 թիվը թվային բազմությանը (գրառումը կատարեք ∈ և ∉ նշանների օգնությամբ):
ա) -2∈[-3;0]
բ) -2∉(-2;3)
գ) -2∈(-∞;-2]
դ) -2∈(-3;+∞)
ե) -2∉N
զ) -2∈Z
է) -2∉Q
ը) -2∉R

4) Անվանեք թվային բազմությանը պատկանող երեք ամբողջ թվեր՝
ա)[0;+∞) — 0, 1, 2
բ)(0;+∞) — 1, 2, 3
գ)(-∞;1) — -3, -2, -1
դ)(-∞;1] — -1, 0, 1

5) Գրառեք նշանակումը և պատկերեք նշված բազմությունները թվային ուղղի վրա՝
ա)2-ից 4 փակ միջակայքի (հատվածի)
բ)2-ից 4 բաց միջակայքի
գ)2-ից 4 կիսաբաց միջակայքի՝ 4-ը ներառած
դ)2-ից 4 կիսաբաց միջակայքի՝ 2-ը ներառած
ե)5-ից +∞ միջակայքի
զ)5-ից +∞ կիսաբաց միջակայքի
է) -∞-ից 0 միջակայքի
ը) -∞-ից 0 կիսաբաց միջակայքի

6) Պատկանու՞մ է արդյոք 2/3 թիվը թվային բազմությանը (գրառումը կատարեք ∈ և ∉ նշանների օգնությամբ):
ա) 2/3∉(0;1]
բ) 2/3∈[1;2]
գ) 2/3∈(-∞;2/3]
դ) 2/3∉(2/3;+∞)
ե) N
զ)Z
է)Q
ը)R

Առաջադրանքներ․
1) Կոորդինատային առանցքի վրա պատկերեք միջակայքը՝
ա)(-2; 7)

բ)(-17; 34)

գ)(1234; 1398)

դ)(-∞; 0)

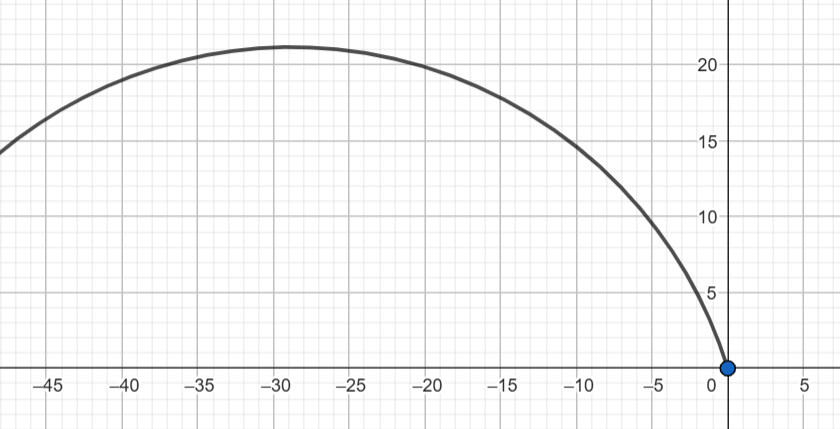
ե)(0; +∞)

զ)(-∞; -3)

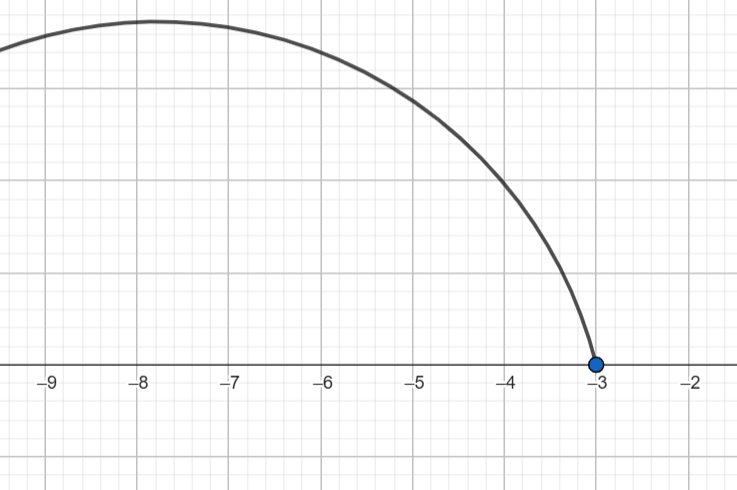
է)(2; +∞)

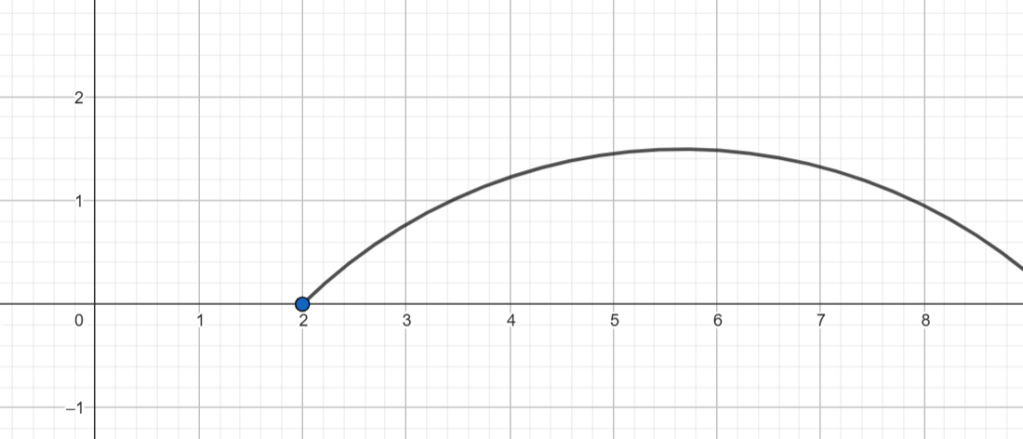
ը)(-∞; +∞)

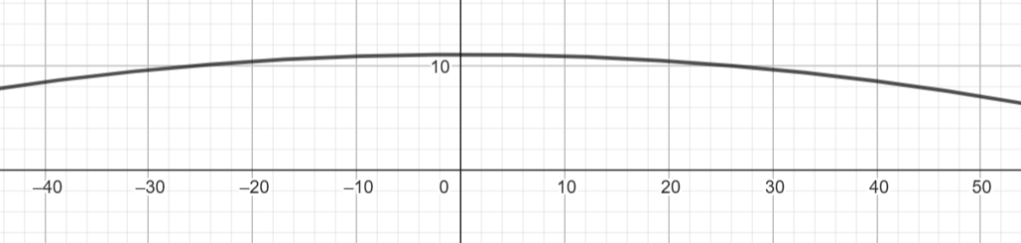
թ)(- 1/3; 0,5)

2) Ինչպիսի՞ նշան (<; =; >) պետք է դնել a և b թվերի միջև, եթե a-b տարբերությունը՝
ա) դրական թիվ է
a>b
բ) բացասական թիվ է
a<b

3) Նկարում պատկերված միջակայքերը գրեք անհավասարությունների նշանների օգնությամբ։

4) Կոորդինատային առանցքի վրա պատկերեք բոլոր այն թվերը, որոնք բավարարում են նշված անհավասարումներին՝
ա)x > 0

բ)x < 3

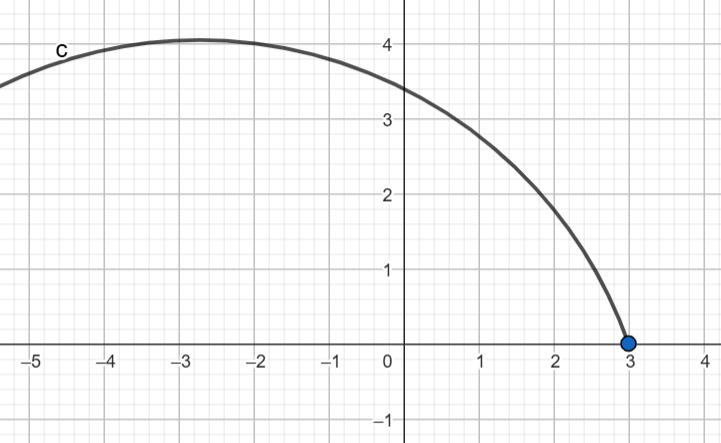
գ)x > 3579
դ)x < -2
ե)x > -1748
զ)x < 0,00006

5) x — a տարբերությունը համեմատեք զրոյի հետ, եթե
ա)x > a — դրական
բ)x < a — բացասական

6) 3 թիվը հանդիսանո՞ւմ է նշված անհավասարման լուծում՝
ա)x > 0 — այո
բ)x > -2 — այո
գ)x < 3,1 — այո
դ)-3 < x < 3 — ոչ
ե)2,(8) < x < 3,1 — այո

Առաջադրանքներ․
1)Նշեք նշված թվերից մեկից մեծ և մյուսից փոքր թիվ։ Պատասխանը գրեք կրկնակի անհավասարության տեսքով`
ա) 3 և 5; 3 > 4 > 5
բ)-25 և-29; -25 > -26 > -29
գ) 2,4 և 2,404; 2,4 < 2,403 < 2,404
դ) 2,5 և 2,6; 2,5 < 2,55 < 2,6
ե)-3,71 և -3,72; -3,71 > -3,715 > -3,72
զ) -0,501 և 0,6; -0,501 < 0,5 < 0,6
2) Տրված ճշմարիտ անհավասարությունից ստացեք նոր ճշմարիտ անհավասարություն՝ գումարելով նրա երկու մասերին միևնույն թիվը՝
ա) 15 < 20, 20 < 25
բ) 1,1 < 1,2, 2,1 < 2,2
գ) 5 > 4, 10 > 9
դ) 1,3 ≥ 1,2, 2,3 ≥ 2,2
ե) 2,5 < 3, 4,5 < 5
զ) 5 ≤ 6, 7 ≤ 8
3) Երկու ճշմարիտ անհավասարությունների հիման վրա կատարեք եզրակացություն։
Օրինակ 3 < 15 և 15 < 20, նշանակում է 3 < 20 :
ա)-5 < 0 և 0 < 2 = -5 < 2
բ) 2 > 1 և 1 > 0 = 2 > 0
գ) -3,7 > -4 և -4 > -7 = -3,7 > -7
դ)-2 < 0 և 0 < 2 = -2 < 2
ե) 2,(1) > 2 և 2 > 1,(6) = 2,1 > 1,6
զ) 0,(5) < 0,(6) և 0,(6) < 0,(67) = 0,5 < 0,67
4) Բազմապատկեք ճշմարիտ թվային անհավասարությունները`
ա) 14 > 10 և 2 > 1 = 28 > 10
բ) 5 > 3 և 6 > 5 = 30 > 15
գ) 6 < 7 և 2 < 3 = 12 < 21
դ) 8 < 9 և 1 < 2 = 8 < 18
5) Գումարեք ճշմարիտ թվային անհավասարությունները՝
ա) 14 > 11 և 10 > 9 = 24 > 20
բ) -2 > -3 և 3 > 2 = 1 > -1
գ) -6 < -5 և 2 < 3 = -4 < -2
դ) -8 < 0 և 8 < 9 = 0 < 1
6) Տրված ճշմարիտ անհավասարությունից ստացեք ճշմարիտ անհավասարություն, որում յուրաքանչյուր թիվ փոխարինված է իր հակադիրով։
Օրինակ, քանի որ 19 > 13, ապա -19 < -13
ա) 3 > 0 = -3 < 0
բ) 5 > -1 = -5 < 1
գ) -9 < -1 = 9 > 1
դ) -5 < -1 = 5 > 1
ե) 9 > -2 = -9 < 2
զ) 0 < 3 = 0 > -3