Առաջադրանքներ․
1) Նման են ABC և A1B1C1 եռանկյունները, եթե AB = 3մ, BC = 4մ, AC = 6մ, A1B1 = 9մ, B1C1 = 12մ , A1C1 = 18մ:
Այո, եթե մի եռանկյան երեք կողմերը համեմատական են մյուս եռանկյան երեք կողմերին, ապա եռանկյունները նման են:
2) Նման են երկու եռանկյուններ, եթե մեկի կողմերը հարաբերում են ինչպես 3:8:9, իսկ մյուսի կողմերը 24 սմ, 9 սմ, 27 սմ են:
3*3=9
3*8=24
3*9=27
3) ABC և BCD եռանկյուններում AB = 36 սմ, BC = 18սմ, AC = 20 սմ, DC = 9սմ, DB = 10 սմ: Ապացուցեք, որ ΔABC ~ ΔBCD :
Այո, նման են։ Եթե մի եռանկյան երկու կողմերը համեմատական են մյուս եռանկյան երկու կողմերին, իսկ այդ կողմերով կազմված անկյունները հավասար են, ապա եռանկյունները նման են։
4) O գագաթով անկյան կողմերից մեկի վրա վերցված են A և B, իսկ մյուսի վրա C և D կետերը այնպես, որ AO = 4 սմ, BO = 7սմ, OC =12 սմ, OD = 21սմ: Նման են OAC և OBD եռանկյունները:
Այո, նման են։
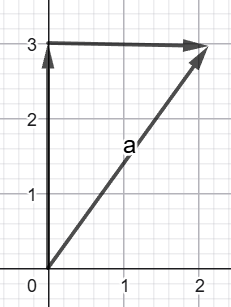
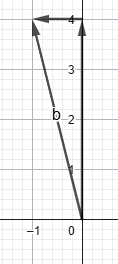
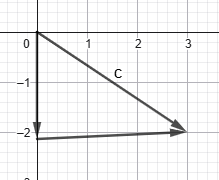
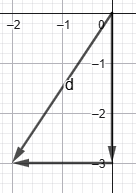
5) Ըստ նկարների տվյալների՝ գտեք x–ը և y–ը։

6) M-ը և N-ը ABC եռանկյան համապատասխանաբար AB և BC կողմերի միջնակետերն են: Ապացուցեք, որ ABC եռանկյունը նման է MBN եռանկյանը: