Հանրահաշիվ՝
Թվային անհավասարությունների հատկությունները
Առաջին աստիճանի մեկ անհայտով անհավասարումներ
Միջակայքերի պատկերումը թվային ուղղի վրա
Առաջին աստիճանի մեկ անհայտով անհավասարումներ
Մեկ անհայտով գծային անհավասարումներ
Մեկ անհայտով գծային անհավասարումների համակարգեր
Մեկ անհայտով գծային անհավասարումների համախմբեր
Թվաբանական քառակուսի արմատ
Թվաբանական քառակուսի արմատ
Երկրաչափություն՝
Շրջանագծի աղեղի աստիճանային չափը
Եռանկյանը ներգծյալ և արտագծյալ շրջանագծեր
Եռանկյանը ներգծյալ և արտագծյալ շրջանագծեր
Քառանկյան ներգծյալ և արտագծյալ շրջանագիծ
Քառանկյան ներգծյալ և արտագծյալ շրջանագիծ
Երկու շրջանագծերի փոխադարձ դասավորությունը
Քառակուսու և ուղղանկյան մակերեսը
Քառակուսու և ուղղանկյան մակերեսը
Քառակուսու և ուղղանկյան մակերեսը
Զուգահեռագծի և շեղանկյան մակերեսը
Զուգահեռագծի և շեղանկյան մակերեսը
Եռանկյան մակերեսը
Рубрика: Երկրաչափություն 8
Եռանկյան մակերեսը
Առաջադրանքներ․
1) Եռանկյան կողմերից մեկը 12 սմ է, դրան տարված բարձրությունը՝ 7 սմ: Գտեք եռանկյան մակերեսը:
S=12*7/2=42սմ2
2) Եռանկյան մակերեսը 108 մմ է, կողմերից մեկը՝ 27 մմ: Գտե՛ք այդ կողմին տարված բարձրությունը:
108*2/27=8
3) Ուղղանկյուն եռանկյան էջերը 7 մ և 16 մ են: Գտե՛ք եռանկյան մակերեսը:
S=7*16/2=56մ2
4) ABC եռանկյունում <B = 90օ , AB = 8 դմ, BC = 15 դմ: Գտեք եռանկյան մակերեսը:
S=8*15/2=60դմ2
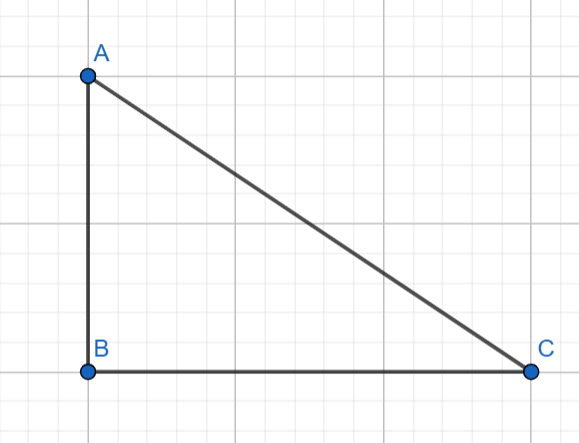
5) Ուղղանկյուն եռանկյան էջերից մեկը երկու անգամ մեծ է մյուսից, մակերեսը 162 սմ է: Գտե՛ք այդ եռանկյան էջերը:
x*2x/2=162
x2=162
x=√162
6) Եռանկյան կողմերից մեկը 9 մ է, մյուսը՝ 6 մ: Առաջին կողմին տարված բարձրությունը 4 մ է: Գտեք երկրորդ կողմին տարված բարձրությունը:
S=9*4/2=18մ2
18*2/6=6մ
7) ABC եռանկյան մեջ <A = 30օ , AB = 14սմ , AC = 6 սմ: Գտեք եռանկյան մակերեսը:
6/2=3սմ
S=3*6/2=9սմ2
8) Ուղղանկյուն եռանկյան էջերը 6 սմ և 8 սմ են, իսկ ներքնաձիգը՝ 10 սմ: Գտեք ներքնաձիգին տարված բարձրությունը:
Զուգահեռագծի և շեղանկյան մակերեսը
1) Զուգահեռագծի սուր անկյունը 30օ է, իսկ բութ անկյան գագաթից տարված բարձրությունները հավասար են 2 սմ և 3 սմ։ Գտեք զուգահեռագծի մակերեսը։
2+2=4
S=4*3=12

2) Գտեք զուգահեռագծի անկյունները, եթե նրա մակերեսը 40 սմ2 է, իսկ կողմերը՝ 10 սմ և 8 սմ։
40/10=4
√8=4
180о-30о=150о
180о-150о=30о
3) Քառակուսին և քառակուսի չհանդիսացող շեղանկյունն ունեն հավասար պարագծեր։ Համեմատեք այդ պատկերների մակերեսները։
4) Գտեք զուգահեռագծի անկյունները, եթե նրա մակերեսը 20 սմ2 է, իսկ բութ անկյան գագաթից կողմերից մեկին տարված բարձրությունը այդ կողմը տրոհում է 2 սմ և 8 սմ երկարությամբ հատվածների՝ սկսած սուր անկյան գագաթից։
2+8=10
20/10=2
2+2=4
45о, 135о, 45о, 135о
5) Համեմատեք ուղղանկյան և զուգահեռագծի մակերեսները, եթե նրանք ունեն հավասար հիմքեր և հավասար պարագծեր։
6) ABCD զուգահեռագծի B անկյունը բութ է։ AD կողմի շարունակության վրա՝ D կետից դեպի աջ նշված է E կետն այնպես, որ <ECD = 60o, <CED = 90o, AB = 4 սմ, AD = 10 սմ։ Գտեք զուգահեռագծի մակերեսը։
7) MPKT զուգահեռագծի MT կողմի վրա նշված է E կետը, <PEM = 90o , <EPT = 45o , ME = 4 սմ, ET = 7 սմ։ Գտեք զուգահեռագծի մակերեսը։
Զուգահեռագծի և շեղանկյան մակերեսը
Առաջադրանքներ․
1) Դիցուք՝ զուգահեռագծի հիմքը a-ն է, բարձրությունը՝ h-ը, իսկ մակերեսը՝ S-ը։ Գտեք՝
ա) S-ը, եթե a = 15 սմ, h = 12 սմ
S=15*12=180սմ2
բ) a-ն, եթե S = 34 սմ2 , h = 8,5 սմ
a=34/8,5=4սմ
գ) h-ը, եթե S = 162 սմ2, a = 9 սմ
h=162/9=18սմ
դ) a-ն, եթե h = 1/2a, S = 21a
a=21a/1a/2=42
2) Զուգահեռագծի անկյունագիծը 13 սմ է և ուղղահայաց է զուգահեռագծի այն կողմին, որը 12 սմ է։ Գտեք զուգահեռագծի մակերեսը։
S=13*12=156սմ2

3) Զուգահեռագծի կից կողմերը հավասար են 12 սմ և 13 սմ, իսկ սուր անկյունը 30o է։ Գտեք զուգահեռագծի մակերեսը։
12/2=6
S=12*6=72սմ2
4) Շեղանկյան կողմը 6 սմ է, իսկ անկյուններից մեկը՝ 150o ։ Գտեք շեղանկյան մակերեսը։
6/2=3
S=6*3=18սմ2
5) Զուգահեռագծի կողմը 8,1 սմ է, իսկ 14 սմ-ի հավասար անկյունագիծը նրա հետ կազմում է 30o անկյուն։ Գտեք զուգահեռագծի մակերեսը։
14/2=7
S=8,1*7=56,7սմ2
6) Դիցուք՝ a-ն և b-ն զուգահեռագծի կից կողմերն են, իսկ h1-ը և h2 -ը՝ բարձրությունները։ Գտեք՝
ա) h2 -ը, եթե a = 18 սմ, b = 30 սմ, h1 = 6 սմ, h2 > h1
S=6*30=180սմ2
h2=180/18=10սմ
բ) h1 -ը, եթե a = 10 սմ, b = 15 սմ, h2 = 6 սմ, h2 > h1
S=6*10=60սմ2
h1=60/15=4սմ
գ) h1 -ը և h2 -ը, եթե մակերեսը՝ S = 54 սմ2 , a = 4,5 սմ, b = 6 սմ
54/4,5=12սմ
54/6=9սմ
Քառակուսու և ուղղանկյան մակերեսը
1) Մի քառակուսու կողմը k անգամ մեծ է մյուս քառակուսու կողմից: Գտե՛ք այդ քառակուսիների մակերեսների հարաբերությունը:
k2a2/a2=k2
2) Քառակուսաձև սենյակներից մեկի կողմը 2 անգամ փոքր է մյուսի կողմից: Գտե՛ք փոքր սենյակի մակերեսը, եթե մեծի մակերեսը 36մ2 է:
6*6=36
6/2=3
S=3*3=9մ2
3) Խոհանոցի պատը երեսապատված է 15 սմ կողմով քառակուսաձև 120 սալիկով: Քանի՞ ուղղանկյունաձև նոր սալիկ է պետք նույն պատը երեսապատելու համար, եթե նոր սալիկների կից կողմերը 10 սմ և 20 սմ են:
S1=15*15=225սմ2
S2=225*120=27000սմ2
S3=10*20=200սմ2
27000/200=135
4) Գտե՛ք 54 սմ պարագծով ուղղանկյան մակերեսը, եթե՝
ա) կից կողմերից մեկը մյուսից մեծ է 3 սմ–ով
3+3=6
54-6=48
48/4=12սմ
12+3=15սմ
S=12*15=180սմ2
բ) կից կողմերը հարաբերում են, ինչպես 4 : 5
18x=54սմ
x=54/18=3սմ
4x=3*4=12սմ
5x=3*5=15սմ
S=12*15=180սմ2
գ) կողմերից մեկը (b + 17) սմ է
P=2x+2b+34
2x+2b=54=34=20
x+b=10
x=10-b
S=(10-b)*(b+17)
5) ABCD ուղղանկյան A անկյան կիսորդը հատում է CD կողմը նրա միջնակետում։ Գտե՛ք ուղղանկյան մակերեսը, եթե AD = 2,5 սմ:
CD=2,5*2=5
S=2,5*5=12,5սմ
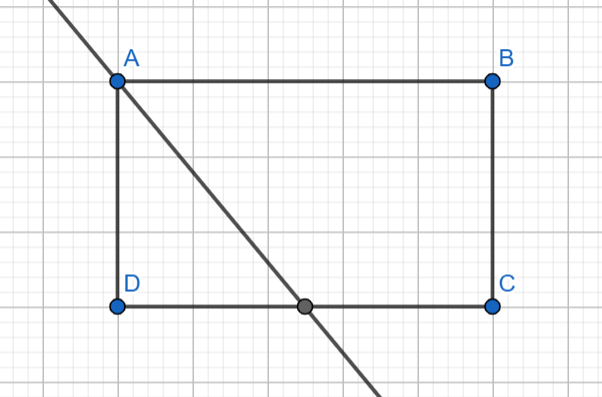
Քառակուսու և ուղղանկյան մակերեսը
Առաջադրանքներ․
1) Քառակուսու պարագիծը 32 սմ է, իսկ ուղղանկյան կողմերից մեկը՝ 45 սմ։ Գտեք այդ ուղղանկյան մյուս կողմը, եթե հայտնի է, որ նրա և քառակուսու մակերեսները հավասար են։
32/4=8
S (քառակուսի)=8*8=64սմ2
64/45
2) Տրված է ABCD քառակուսին։ AD ճառագայթի վրա վերցված է M կետն այնպես, որ <AMB=30o, և BM=20 սմ։ Գտեք այդ քառակուսու մակերեսը։
20/2=10
S=10*10=100սմ2
3) Անհրաժեշտ է սենյակի՝ 5,5 մ և 6 մ կողմերով ուղղանկյունաձև հատակը ծածկել մանրահատակով։ Դրա համար քանի՞ մանրահատակ կպահանջվի, եթե այդ տախտակներից յուրաքանչյուրն ունի 30 սմ երկարությամբ և 5 սմ լայնությամբ ուղղանկյան ձև։
S=550*600=330000սմ2
S=30*5=150սմ2
330000/150=2200
4) ABCD ուղղանկյան A անկյան կիսորդը BC կողմը հատում է K կետում։Հայտնի է, որ BK=5սմ , KC=7սմ։ Գտեք այդ ուղղանկյան մակերեսը։
5+7=12սմ
S=12*5=60սմ2

5) 15 սմ կողմով քառակուսաձև քանի՞ սալիկ կպահանջվի, որպեսզի երեսպատվի 3մ և 2,7մ կողմերով ուղղանկյունաձև պատը։
S=300*270=81000սմ2
S=15*15=225սմ2
81000/225=360
Քառակուսու և ուղղանկյան մակերեսը
Առաջադրանքներ․
1) Գտեք քառակուսու մակերեսը, եթե նրա կողմը հավասար է՝
ա) 1,2 սմ
S=1,2*1,2=1,44սմ2
բ) 3/4 դմ
S=3/4*3/4=9/16դմ2
գ) 3ամբ․1/3 մ
S=10/3*10/3=100/9մ2
2) Ինչպե՞ս կփոխվի քառակուսու մակերեսը, եթե նրա կողմերը՝
ա) մեծացվեն 3 անգամ
Կմեծանա 9 անգամ
բ) փոքրացվեն 2 անգամ
Կփոքրանա 4 անգամ
3) Ուղղանկյան կից կողմերը հարաբերում են, ինչպես 4:3, իսկ նրա պարագիծը 28 սմ է։ Գտեք այդ ուղղանկյան մակերեսը։
2*7x=28
14x=28
x=28/14=2
S=8*6=48սմ2
4) Որոշեք այն քառակուսու կողմը, որի մակերեսը հավասար է՝
ա) 16 սմ2
4սմ
բ) 25 սմ2
5սմ
գ) 2,25 սմ2
1,5սմ
5) Դիցուք՝ ուղղանկյան կից կողմերն են a-ն b-ն, իսկ մակերեսը՝ S-ը։ Գտեք՝
ա) S-ը, եթե a=8,5 սմ, b=3,2 սմ
S=8,5*3,2=27,2սմ
բ) S-ը a=2/3 սմ, b=1,2սմ
S=2/3*1,2=4/5սմ
գ) b-ն, եթե a=32 սմ, S=684 սմ2
b=684/32=171/8սմ
դ) a-ն, եթե b=4,5 դմ, S=1215 սմ2
a=1215/4,5=27սմ
6) Ուղղանկյան կողմերից մեկը 12 սմ է, իսկ մակերեսը՝ 96 սմ2։ Գտեք այդ ուղղանկյան պարագիծը։
96/12=8
P=12*2+8*2=40սմ
Երկու շրջանագծերի փոխադարձ դասավորությունը
Առաջադրանքներ․
1) Տրված են երկու շրջանագծեր, որոնք ունեն մեկ ընդհանուր կետ:
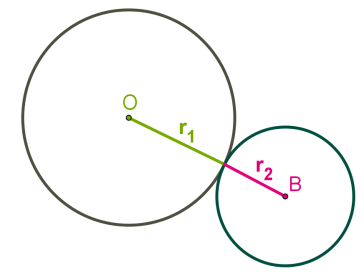
r1-ը և r2-ը համապատասխանաբար մեծ և փոքր շրջանագծերի շառավիղներն են:
Ընտրիր ճիշտ պնդումը:
1. OB>r1+r2
2. r1+r2=OB
3. r1+r2>OB
2) Տրված են հետևյալ երկու շրջանագծերը, որոնք ընդհանուր կետեր չունեն:

r1-ը և r2-ը համապատասխանաբար մեծ և փոքր շրջանագծերի շառավիղներն են:
Ընտրիր ճիշտ պնդումը:
1. r1−r2=AC
2. AC<r1−r2
3. AC=r1+r2
3) Գտիր ED-ն, եթե AC= 4 սմ, իսկ շրջանագծերի կենտրոնների միջև հեռավորությունը 5 սմ է:

4) Գծիր տրված O և B կենտրոններով մեկ ընդհանուր կետ ունեցող շրջանագծեր, որոնց շառավիղները հավասար են՝ r1=28 սմ և r2=10 սմ: Հաշվիր OB հեռավորությունը:
Քառանկյան ներգծյալ և արտագծյալ շրջանագիծ
1) Շրջանագծին ներգծած է ABCD քառանկյունը, որի մեջ <A=104o և <B=71o։ Գտեք անկյուններ C-ն և D-ն։
180-104=76o
<D=76o
180-71=109o
<C=109o

2) Արդյոք կարելի՞ է տրված ABCD քառանկյանը արտագծել շրջանագիծ, եթե՝
ա)<A=64o, <B=95o, <C=106o — ոչ
բ)<A=72o, <B=69o, <D=111o — այո
գ)<A=90o, <C=90o, <D=80o — ոչ
դ)<A=2α, <B=5αo, <C=7αo ,<D=4α — ոչ
3)

<N=180-75=105o
<M=180-53=127o
4) Տրված է MK+EF=40: PMEFK -?

PMEFK=40*2=80
5) Տրված է NE=MF: EF+MN -?

4*4=16
Քառանկյան ներգծյալ և արտագծյալ շրջանագիծ
Առաջադրանքներ․
1) Շրջանագծին արտագծած հավասարասրուն սեղանի հիմքերը հավասար են 2սմ և 8սմ։ Գտեք սեղանի պարագիծը։
P=2*(2+8)=20սմ
2) Շրջանագծին արտագծած հավասարասրուն սեղանի հիմքերից մեկը հավասար է մյուսի եռապատիկին, իսկ սեղանի սրունքը 8սմ է։ Գտեք սեղանի հիմքերը։
CD=3AB
AC, BD=8սմ
8*2=16
16/4=4
AB=4սմ
CD=12սմ
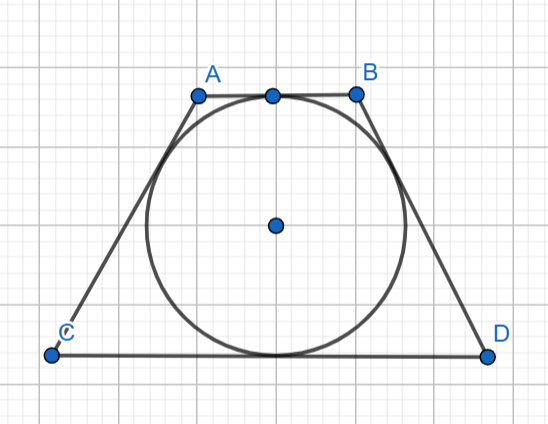
3) Գտեք շրջանագծին արտագծած հավասարասրուն սեղանի կողմերը, եթե նրա պարագիծը 40սմ է, իսկ հիմքերից մեկը 4 անգամ փոքր է մյուսից։
4AB=CD
40/2=20
AC, BD=10սմ
20/5=4
AB=4սմ
CD=16սմ
4) Հավասարասրուն սեղանին ներգծած է շրջանագիծ։ Այդ սեղանի պարագիծը 60սմ է։ Գտեք նրա սրունքը։
60/2=30
30/2=15
սրունքեր=15սմ
5) Հավասարասրուն սեղանի սրունքը 8սմ է, իսկ փոքր հիմքին առընթեր անկյունների գումարը՝ 300օ ։ Գտեք այդ սեղանին ներգծած շրջանագծի շառավիղը։
