Խնդիրներ

223․ 180-32=148
148:2=74
74+32=106
∠=74^о, ∠=106^о

224. Քանի որ ABC և CDE եռանկյունները հավասար են, BC=DE, և AB և DC ուղղիղները հատվում են AE ուղղով, AB | | CD

225. Քանի որ ∠ABK=∠BM
KM=MB
∠MKB=∠ABK
∠B=∠K, ուղիղները զուգահեռ են

226. ∠A=40^o
∠BCE=80^o
Քանի որ MC-ն BCE անկյան կիսորդն է, ∠ACM=∠MCE=40^o=∠BAC
AB| |CM

227. ∠A=40^o
∠B=70^o
∠C=70^o
Քանի որ BC ճառագայթը ABD անկյան կիսորդն է, ∠ABC=∠CBD=∠ACB
∠ACB=∠CBD, դրա համար էլ AC| |BD

Դասարանում

183. P=15, BC=AB+2, AB=AC-1, AC=AB+1, BC=x+2
P=AB+BC+AC=x+x+1+x+2
P=3x+3
3x+3=15
3x=15-3=12
12:3=4
x=4
AB=4
AC=5
BC=6
184․
BC=AB+2
AB+AC=BC+3
AB=x
AC=x
BC=x+2
x+x=x+2+3=x2=x+5
x=5
x+2=7
AB=AC=5
BC=7
185.  P ABD=P BCD+2
BC=8
AB=x
AC=x
2x+x+BD=x+8+BD
2x=8
x=4
AB=AC=2×4=8

Դասարանում

210.
P ABC=24սմ
P ACD=20սմ
P CPD=12սմ
CD=?
CD-ն ընդանուր է
20+12=32
32-24=8
8:2=4

211. P ABC=47սմ
BC=AB+3սմ
BC=AC-5սմ


212. Ըստ եռանկյան հավասարության առաջին հայտանիշի՝ եթե մի եռանկյան երկու կողմերը և դրանցով կազմված անկյունը համապատասխանաբար հավասար են մյուս եռանկյան երկու կողմերին և դրանցով կազմված անկյանը, ապա այդպիսի եռանկյունները հավասար են:

Տանը

1. Հավասարասրուն եռանկյան կողմերն են 10 սմ և 22 սմ: Գտեք այդ եռանկյան պարագիծը:
P=10+22+10=42
P=10+22+22=54
2. Հավասարասրուն եռանկյան հիմքը 5 սմ-ով մեծ է սրունքից, իսկ պարագիծը 44 սմ է: Գտեք եռանկյան կողմերը:
x+x+x+5=44
44-5=3x
39=3x
x=13
x+5=18
13+13+18=44
3. Հավասարասրուն եռանկյան հիմքը 5 անգամ մեծ է սրունքից, իսկ պարագիծը 63 սմ է: Գտեք եռանկյան կողմերը:
4. Հավասարասրուն եռանկյան հիմքը 4 անգամ փոքր է սրունքից, իսկ պարագիծը 96 սմ է: Գտեք եռանկյան կողմերը:
6x=96
x=96:6=16
16×4=64
96-64=32
32:2=16
16+16+64
5. Բութանկյուն հավասարասրուն եռանկյան պարագիծը 46 սմ է, իսկ նրա կողմերից մեկը մյուսից մեծ է 4 սմ–ով: Գտեք եռանկյան կողմերը։
x+x+x+4=46
46-4=3x
42=3x
x=14
x+4=18
14+14+18=46

Կրկնողության հարցեր

1. Բացատրեք, թե որ պատկերն է կոչվում եռանկյուն: Գծագրեք եռանկյուն և ցույց տվեք նրա կողմերը, գագաթները և անկյունները: Ի՞նչ է եռանկյան պարագիծը:
Եռանկյուն կոչվում է այն երկրաչափական պատկերը, որը ունի 3 կողմն, 3 գագաթ և 3 անկյուն։
2. Ո՞ր եռանկյուններն են կոչվում հավասար:
Հավասար կոչվում է այն երկրաչափական պատկերը, որի երեք կողմերը, գագաթները և անկյունները հավասար են։
3․ Ձևակերպեք եռանկյունների հավասարության առաջին հայտանիշն արտահայտող թեորեմը։
Եթե եռանկյան երկու կողմն և նրանցով կազմած անկյունը հավասար են մյուս երանկյան երկու կողմն և նրանցով կազմած անկյանը, ապա եռանկյունները հավասար են։
4. Բացատրեք, թե որ հատվածն է կոչվում տրված կետից տրված ուղղին տարված ուղղահայաց։
Այն հատվածը, որը տրված ուղղիով կազմում է 90 ^օ անկյուն։
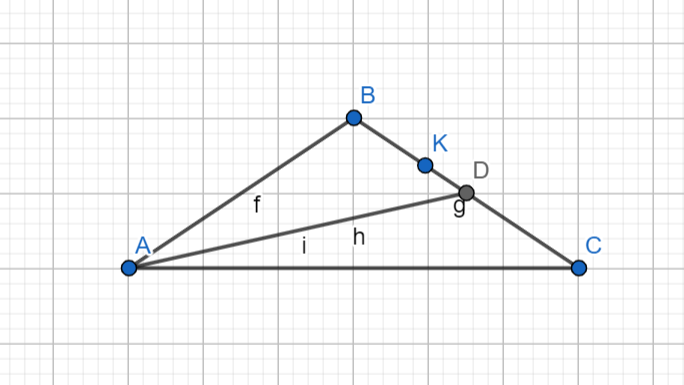
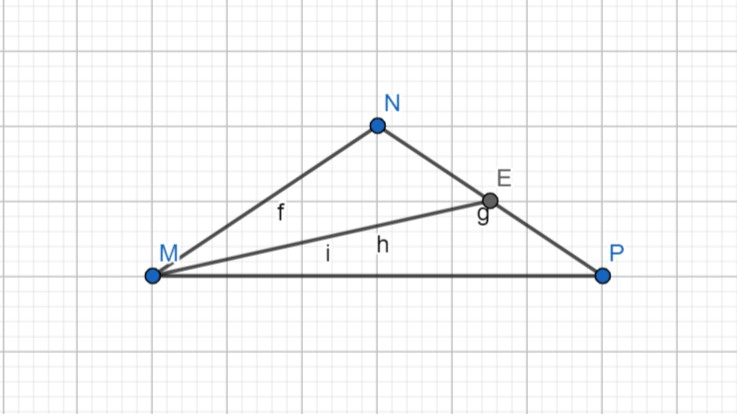
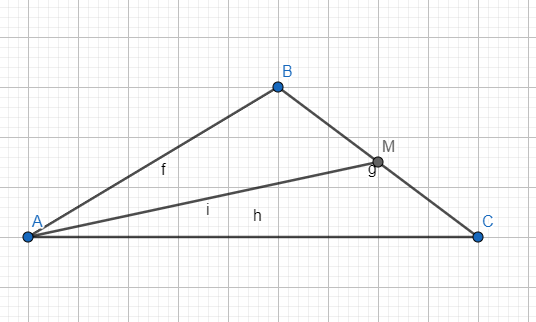
5. Ո՞ր հատվածն է կոչվում եռանկյան միջնագիծ: Եռանկյունը քանի՞ միջնագիծ ունի:
Եռանկյան գագաթը հանդիպակաց կողմի միջնակետի հետ միացնող հատվածը կոչվում է եռանկյան միջնագիծ: Եռանկյունը ունի 3 միջագիծ։
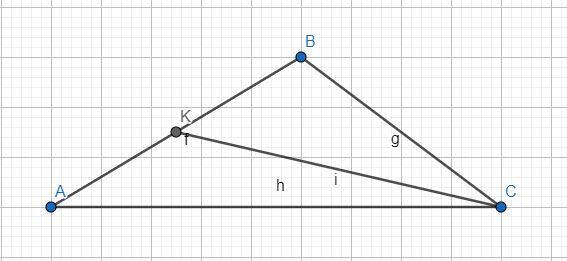
6. Ո՞ր հատվածն է կոչվում եռանկյան կիսորդ։ Եռանկյունը քանի՞ կիսորդ ունի:
Կիսորդ են կոչում եռանկյան այն հատվածը, որը կիսում է եռանկյունը։ Եռանկյունը ունի 3 կիսորդ։
7. Ո՞ր հատվածն է կոչվում եռանկյան բարձրություն: Եռանկյունը քանի՞ բարձրություն ունի:
Եռանկյան ուղղահայաց հատվածը կոչվում է եռանկյան բարձրություն։ Եռանկյունը ունի 1 բարձրություն։
8. Ո՞ր եռանկյունն է կոչվում հավասարասրուն: Ինչպե՞ս են կոչվում նրա կողմերը։
Հավասարասրում եռանկյուն է կոչվում այն պատկերը, որի 2 կողմերը հասավար են։ Հավասարասրոն եռանկյան 2 հավասար կողղմերը կոչվում են սրունք, իսկ մյուս կողմը կոչվում է հիմք։
9. Ո՞ր եռանկյունն է կոչվում հավասարակողմ։
Եռանկյուն, որի 3 կողմերը հավասար են, կոչվում է հավասարակողմ եռանկյուն։
10․ Ապացուցեք, որ հավասարասրուն եռանկյան հիմքին առընթեր անկյունները հավասար են:
11. Ձևակերպեք և ապացուցեք թեորեմ՝ հավասարասրուն եռանկյան կիսորդի մասին:

Դասարանում

163.
P=29
29-12=17
17:2=8,5
AB=8,5սմ

164.
P=75
75:3=25
սրունք=50սմ
հիմք=25սմ

165․

Տանը

Դասարանում

152. P=10+10+17=37
153.
x + x + x + 4 = 37
37 – 4 = 3x
33 = 3x
x = 11
x+4=15
154.
AB=15
BC=15
AC=15
P=15×3
P=45
155.
60:3=20դմ
156.
AB=BC
A=40^o
C=40^o
157.

Տանը

158. Ոչ, հնարավոր չէ։
159.

1.Բութանկյուն հավասարասրուն եռանկյան պարագիծը 45 սմ է, իսկ նրա կողմերից մեկը մյուսից մեծ է 9 սմ–ով: Գտեք եռանկյան կողմերը։
45-9=36
36:3=12
12+9=21
AC=21սմ
BC=12սմ
AB=12սմ
2.BC հիմքով ABC հավասարասրուն եռանկյան պարագիծը 40 սմ է, իսկ սրունքը հիմքից մեծ է երկու անգամ: Գտեք եռանկյան կողմերը։
2x+2x+x=5x
40:5=8
8+8=16
հիմք=8սմ
սրունքները=16սմ
3.BK ն AC հիմքով հավասարասրուն եռանկյան կիսորդն է, ընդ որում՝ AK = 6,8 սմ: Գտեք AC-ն:

4.BD — ն AC հիմքով հավասարասրուն եռանկյան միջնագիծն է, ընդ որում <ABD = 26⁰: Գտեք <B-ն:
26×2=52^o
5.BC հիմքով ABC հավասարասրուն եռանկյան մեջ տարված է AM միջնագիծը։ Գտեք այդ միջնագիծը, եթե ABC եռանկյան պարագիծը 30 սմ է, իսկ ABM եռանկյան պարագիծը՝ 20 սմ:
40=2am+(ac+bc+ab=30)սմ
2am+30=40սմ
2am=10սմ
am=5սմ

Դասարանում

160. AK=5,6սմ
AC=2xAK=5,6+5,6=11,2սմ

161.
B=ABDx2=26×2=52^o
B=52^o
162. P=10+7+10=27սմ
163.
29-12=17
AB=17:2=8,5
AB=8,5սմ

Դասարանում

135. BK+KD=5+2=7դմ
BC=2 x BD=2×7=14դմ

BD=5-2=3դմ
DC=2BD=2×3=6դմ

136.

137.

138. BAM=A+B=33+42=75^o
BCK=C+B=36+42=78^o
NBC=C+B=21+72=93^o

Տանը