1) Oxy հարթության վրա շրջանագիծը տրված է հետևյալ հավասարումով. Ինչի՞ են հավասար շրջանագծի կենտրոնի կոորդինատները և շառավիղը:
ա) x2 +y2 =36
O (0;0), R=6
բ) (x — 3)2 + (y — 5)2 = 25
O (3;5), R=5
2) Շրջանագիծը տրված է (x + 4)2 + (y — 3)2 = 2,56 հավասարումով: Նշե՛ք, թե (-4, 4), (-2, 1), (-2, 3), (-5, 4) կետերից որոնք են ընկած`
ա) շրջանագծի վրա
Ոչ մի կետ
բ) տրված շրջանագծով եզերված շրջանի ներսում
(-4;4)
գ) տրված շրջանագծով եզերված շրջանից դուրս
(-2;1), (-2;3)
3) Գրե՛ք r շառավիղով և O կենտրոնով շրջանագծի հավասարումը, եթե`
ա) r = 1, O(0, -7)
(x-0)2+(y-7)2=12
բ) r = 5, O(1, -2)
(x-1)2+(y+2)2=52
գ) r = 0,5, O(-3, -7)
(x+3)2+(y+7)2=0,52
4) Գրե՛ք այն շրջանագծի հավասարումը, որի կենտրոնը կոորդինատների սկզբնակետն է, և որն անցնում է՝
ա) (1, 2)
(x-1)2+(y-2)2=52
բ) (-3, 5)
(x+3)2+(y-5)2=342
գ) (4, -3) կետով
(x-4)2+(y+3)2=232
5) Գրե՛ք M կենտրոնով և N կետով անցնող շրջանագծի հավասարումը, եթե՝
ա) M(−1, 2), N(0, 5)
բ) M(0, 3), N(-2, 6)
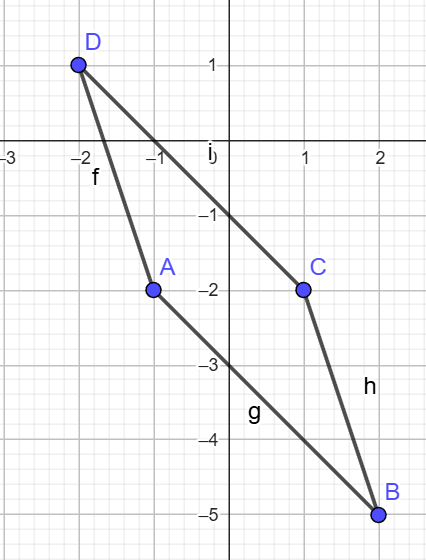
6) Գտե՛ք A(-1,-2), B(2, −5), C(1, -2), D(-2, 1) գագաթներով ABCD զուգահեռագծի պարագիծը և անկյունագծերը:
AB=√(2+1)2+(-5+2)2=√18
BC=√(1-2)2+(-2+5)2=√10
CD=√(-2-1)2+(1+2)2=√18
DA=√(-1+2)2+(-2-1)2=√10
P=(√18*2)+(√10*2)≈14,8
୨ৎ Արփի Փիրումյան 𝜗ৎ 